[평범한 학부생이 하는 논문 리뷰] One Step Diffusion via Shortcut Models (ICLR 2025 oral)

paper : https://arxiv.org/abs/2410.12557

One Step Diffusion via Shortcut Models

Abstract

본 논문은 shortcut model을 제안한다. 이는 single network를 통해 one or multiple step을 통해 image generation을 하는 모델이다. Shortcut model은 현재의 noise level뿐만 아니라 원하는 step size를 condition으로 받는데, 이는 generation process에서 앞으로 skip하는 것을 가능하게 한다. 광범위한 sampling step budgets에 대해서, 일관적으로 고퀄리티의 이미지를 생성한다.

$\rightarrow$ 기존 diffusion과 flow matching model에서의 expensive inference를 해결하려 한다.

1. Shortcut Models for Few Step Generation

 본 논문은 diffusion과 flow-matching model에 필요로 되는 다수의 sampling steps를 극복하는 새로운 model인 shortcut model을 제안한다. Key intuition은 model을 timestep $t$뿐만 아니라 desired step size $d$로 model을 conditioning함으로써 다른 sampling budgets를 지원하는 single model을 학습할 수 있다는 것이다.

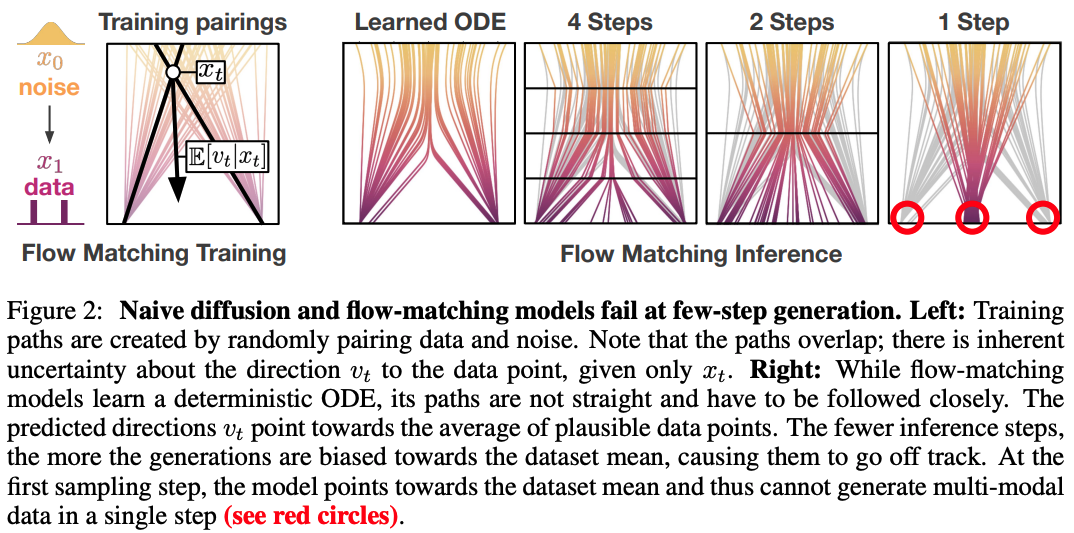
위 그림에서와 같이, flow-matching은 noise와 data를 curved path로 mapping하는 ODE를 학습한다. 단순히 큰 sampling step을 취하는 것은 큰 discretization error를 야기하고 single-step의 경우에는 catastrophic failure를 야기한다. $d$에 대해 conditioning하는 것은 shortcut model이 미래의 curvature를 고려하도록 하고 경로를 벗어나지 않게 정확한 다음 지점으로 점프하도록 한다. $x_t$에서 정확한 다음 지점 $x^\prime_{t+d}$로의 normalized direction을 다음과 같이 나타낸다.

본 논문은 shortcut model $s_\theta(x_t,t,d)$이 모든 조합의 $x_t, t, d$에 대한 shortcut을 학습하는 것을 목표로 한다. Shortcut model은 flow-matching model의 larger step size로의 일반화로 보일 수 있다.

 본 논문은 shortcut model에 내제된 하나의 shortcut step은 반 사이즈의 두개의 연속적인 shortcut step과 동일하다는 self-consistency property를 활용한다.

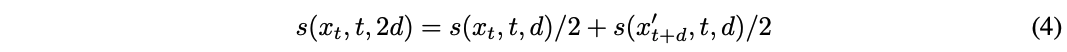
이는 shortcut model이 $d > 0$에 대한 self-consistency target을 사용하고 $d = 0$에 대한 base case로 다음 flow-matching loss를 사용하도록 한다.

원칙적으로는, 어떤 분포 $d \sim p(d)$에 대해서도 model을 학습할 수 있다. 실제로는, $d=0$으로 학습되는 부분과 랜덤하게 샘플된 $d > 0$ target으로 학습되는 부분으로 batch를 나눈다. Shortcut model loss는 다음과 같다.

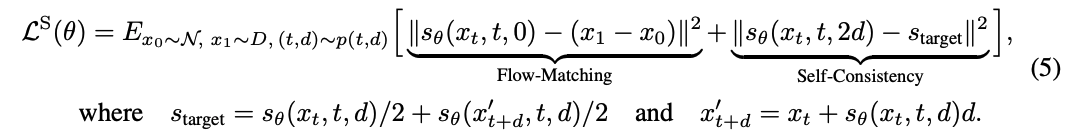
위의 objective는 single step을 포함한 어떤 step size의 sequence에 대해서도 일관된 noise to data mapping을 학습한다. Flow matching 부분에서, 작은 step size에서 empirical velocity sample을 matching하도록 한다. 이는 shortcut model이 많은 step에서 기본 generation 능력을 개발하도록 한다. Self-consistency 부분에서, 더 큰 step-size에 대해 적절한 target이 두 개의 더 작은 shorcut의 sequence를 concat함으로써 구성된다. 이는 생성 능력을 multi-step에서 few-step, one-step으로 전달한다. 이 결합된 objective는 single model을 사용해서 하나의 end-to-end 학습 과정으로 같이 학습될 수 있다.

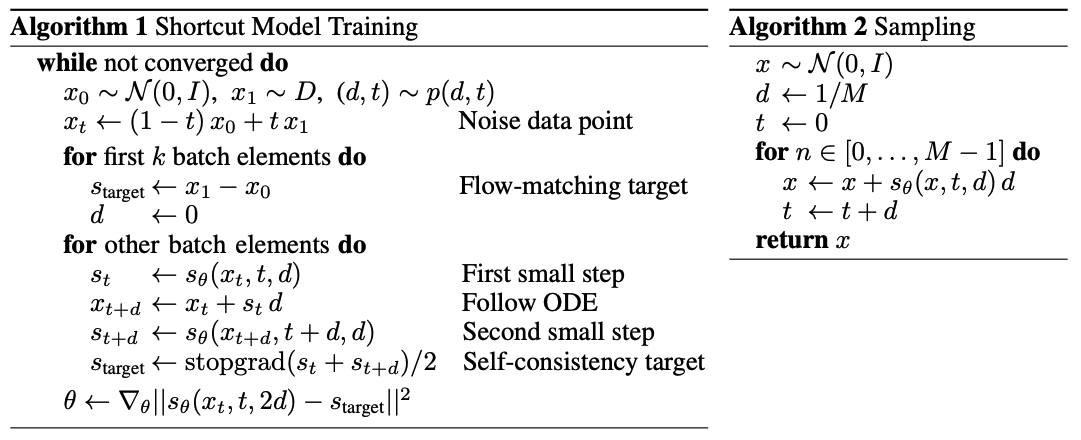
1.1 Training Details

Regressing onto empirical samples

 $d \rightarrow 0$에서, shortcut은 순간적인 flow와 동등하다. 그러므로, (2)를 이용해서 $d = 0$에서 shortcut model을 학습할 수 있다. 이 term은 data denoising ODE를 매칭하는 small-step shortcuts에 대한 기준점으로 볼 수 있다. $t \sim U(0,1)$에서 균등하게 샘플링하는 것이 가장 간단하고 잘 작동한다고 한다.

Enforcing self-consistency

 Shortcut model이 small step-size에서 정확하다는게 주어지면, 다음 목표는 shortcut model이 이 경향을 larger step-size에서도 유지하도록 보장하는 것이다. 이를 위해서 본 논문은 self-generated bootstrap targets에 의존한다.

Compounding approximation error를 제한하기 위해서, 본 논문은 위 그림과 같이 binary recursive formulation을 선택한다.

 본 논문은 스탭 수 $M$을 128로 설정한다. 학습 동안, $x_t, t, \text{random} \ d < 1$를 샘플하고 shortcut model을 가지고 두 sequential steps를 취한다. 이 두 step들의 concatenation은 $2d$에서 model을 학습시키기 위한 target으로 사용된다.

 두번째 step은 empirical data pairing이 아닌 denoising step ODE하에서 $x^\prime_{t+d}$가 query된다.

Joint optimization

(5)은 empirical flow-matching objective와 self-consistency objective로 구성되고 이는 training동안에 joint하게 optimize된다. Empirical term의 분산이 더 큰데, 이는 self-consistency term은 deterministic bootstrap targets를 사용하는 반면 empirical term은 내재적인 불확실성을 가지고 random noise pairing에 regress하기 때문이다. 본 논문은 empirical target에 더 큰 batch를 사용하는 것이 도움이 된다는 것을 발견한다.

 학습은 self-consistency term을 덜 요구하고, 이게 더 비싸기 때문에 위의 behavior는 computational efficiency에 대한 여지를 준다. 본 논문은 $1-k$ empirical targets과 $k$ self-consistency targets의 비율을 사용한다. 여기서 $k = 1/4$가 합리적이라고 한다.

Guidance

 본 논문은 CFG가 small step size에서는 도움이 되지만 linear approximation이 적절하지 않을 때 larget step에서 error-prone하다는 것을 발견한다. 그래서 CFG를 $d = 0$에서 shortcut model을 평가할 때 사용하고 다른 때에는 사용하지 않는다. Shortcut model에서 CFG의 한계는 CFG scale이 training 전에 구체화돼야 한다는 것이다.

Exponential moving average weights

 EMA는 generation에 대해 smoothing 효과를 가져온다. Shortcut model에서도 유사하게, $d = 0$에서 loss로부터의 variance는 $d = 1$에서 output에서 큰 잡음을 야기한다. Self-consistency target을 생성에 대해 EMA 파라미터를 사용하는 것은 이 문제를 완화한다.

Weight decay

 본 논문에서는 특히 early training step에서 weight decay가 안정성에 중요하다는 것을 발견한다. 초기 모델에서, 이 모델이 생성하는 self-consistency target들은 거의 noise이다. 이는 artifact와 bad feature learning을 야기한다. 본 논문은 적절한 weight deacy가 이러한 문제를 없앨 수 있고 discretization schedulers나 careful warmups에 대한 필요를 우회할 수 있게 한다는 것을 발견한다.

Discrete time sampling

실제로, 본 논문은 연관된 timestep에 대해서만 학습함으로써 shortcut network의 짐을 줄일 수 있다. 학습 동안, $d$를 먼저 샘플링하고 $d$의 배수와 같이 shortcut model이 query될 discrete point에 대해서만 $t$를 샘플링한다. 그리고 이 timestep들에 대해서만 self-consistency objective를 학습한다.

2. Experiments

2.1 How do shortcut models compare to prior one-step generation methods?

2.2 What is the behavior of shortcut models under varying inference budgets?

2.3 How does shortcut model performance increase with model scale?

2.4 Can shortcut models give us an interpolatable latent space?

Noise point의 pair $(x^0_0, x^1_0)$을 샘플링하고 다음과 같이 interpolate한다.

그 결과는 아래와 같다.

2.5 Do shortcut models work in non-image domains?