| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- rectified flow matching models
- Machine Unlearning
- video generation
- VirtualTryON
- visiontransformer
- rectified flow
- Concept Erasure
- BOJ
- image editing
- flow matching
- flow models
- 네이버 부스트캠프 ai tech 6기
- diffusion
- memorization
- unlearning
- 3d generation
- ddim inversion
- 코테
- inversion
- rectified flow models
- image generation
- 프로그래머스
- Python
- diffusion model
- diffusion models
- video editing
- Programmers
- 3d editing
- flow matching models
- 논문리뷰
- Today
- Total
평범한 필기장
[평범한 대학원생이 하는 논문 간단 요약] Selective Amnesia: A Continual Learning Approach to Forgetting in Deep Generative Models (NeurIPS 2023) 본문
[평범한 대학원생이 하는 논문 간단 요약] Selective Amnesia: A Continual Learning Approach to Forgetting in Deep Generative Models (NeurIPS 2023)
junseok-rh 2025. 9. 15. 16:34Paper : https://arxiv.org/abs/2305.10120
Selective Amnesia: A Continual Learning Approach to Forgetting in Deep Generative Models
The recent proliferation of large-scale text-to-image models has led to growing concerns that such models may be misused to generate harmful, misleading, and inappropriate content. Motivated by this issue, we derive a technique inspired by continual learni
arxiv.org
Abstract
이미지 생성 모델에서 선택적으로 concept을 지우는 매서드인 Selective Amnesia를 제안한다.
1. Selective Amnesia
본 논문은 model을 $D_r \vert \mathbf{c}_f$를 생성하는 것은 기억하면서 $D_f \vert \mathbf{c}_f$에 대해서 생성하는 것을 forget하도록 학습하는 것을 목표로 한다. Key criteria는 training process가 $D$에 대한 접근을 필요로 하지 않는 것이다.
A Bayesian Continual Learning Approach to Forgetting
본 논문은 Elastic Weight Consolidation (EWC)에서 영감을 받은 Continual Learning의 Bayesian 관점으로부터 시작한다.

Forgetting을 위해서, $D_r$에 대해서만 condition된 posterior만 보자면 다음과 같다.

여기서 $\log p(D_f \vert \theta) = \log p(\mathbf{x}_f, \mathbf{c}_f \vert \theta) = \log p(\mathbf{x}_f \vert \theta, \mathbf{c}_f) + \log p(\mathbf{c}_f)$이고, $\log p(\theta \vert D_f, D_r)$은 EWC의 Laplace approximation으로 대체한다. 본 논문의 목표는 maximum a pasteriori estimate을 얻기 위해서 $\log p(\theta \vert D_r)$를 최대화하는 것이다. 직관적으로, (1)을 최대화하는 것은 $\theta$를 $\theta^*$와 가깝게 유지하면서 likelihood $\log p(\mathbf{x}_f \vert \theta, \mathbf{c}_f)$를 낮추는 것이다.
Direct optimization에는 다음 두 가지 문제점이 있다.
- (1)은 $D_r$로부터의 sample을 사용하는 것을 포함하지 않는다. 이는 시간이 지남에 따라 기억되야할 data를 생성하는 모델의 능력을 감소시킨다.
- Variational model에 집중하는데 이는 log-likelihood가 intractable하다. ELBO를 알지만 이를 최소화하는 것은 log-likelihood를 필수적으로 감소시키지는 않는다.
본 논문은 위 두 가지 문제점을 replay와 surrogate objective를 통해서 해결한다.
1.1 Generative Replay Over $D_r$
본 논문의 approach는 continual learning의 두 패러다임인 EWC와 GR를 통합해서 single objective로 optimize될 수 있다는 것이다. 본 논문은 $D_r$의 posterior에 대한 optimization은 유지하면서, generative replay term에 대응되는 $D_r$에 대한 extra likelihood term을 도입한다.

$\log p(\theta)$ term은 파라미터 $\theta$에 대한 prior에 대응된다. 본 논문은 $\log p(\theta)$를 optimization에 대해서는 상수로 둬도 좋은 결과를 보인다는 것을 발견했다. 전체적인 objective는 다음과 같이 쓰여진다.

(3)에서의 기댓값들은 모델을 통해 생성된 샘플들을 이용해서 approximation한다. 유사하게 Fisher Information Matrix (FIM)인 $F$ 또한 model을 통해 생성된 샘플들로 계산된다. 그러므로 (3)은 original training dataset $D$ 없이 optimize될 수 있다. GR term의 추가는 $D_f$를 잊도록 학습한 후에 $D_r$을 생성할 때 성능을 향상시킨다.
1.2 Surrogate Objective
(1)과 유사하게, (3) 또한 잊어야할 데이터의 log-likelihood를 낮출 필요가 있다. ELBO밖에 모르는데, naive하게 ELBO로 likelihood term을 대체하는 것은 안 좋은 결과를 이끈다.
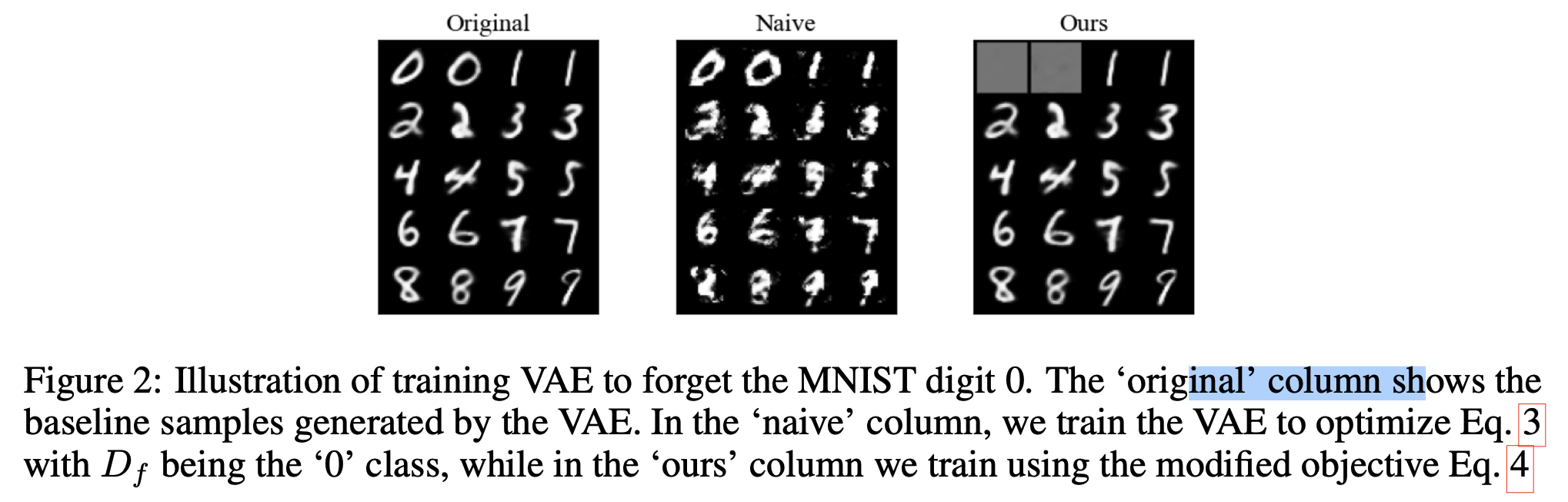
본 논문은 $\theta^*$로 parameterize된 original model과 비교해서 $D_f$의 더 낮은 log-likelihood가 보장되는 alternative objective를 제안한다. ELBO나 log-likelihood를 직접 최소화하기보다는, 본 논문은 잊어야할 class의 surrogate distribution의 log-likelihood를 최대화한다.($q(\mathbf{x} \vert \mathbf{c}_f) \neq p(\mathbf{x} \vert \mathbf{c}_f)$)

Theorem 1은 surrogate objective $\arg \max_\theta \mathbb{E}_{q(\mathbf{x}\vert\mathbf{c})p_f(\mathbf{c})}[\log p (\mathbf{x} \vert \theta, \mathbf{c})]$를 optimize하는 것은 original starting point $\theta^*$로부터 $\mathbb{E}_{p(\mathbf{x} \vert \mathbf{c})p_f(\mathbf{c})}[\log p(\mathbf{x} \vert \theta, \mathbf{c})]$를 줄이는 것을 보장한다.
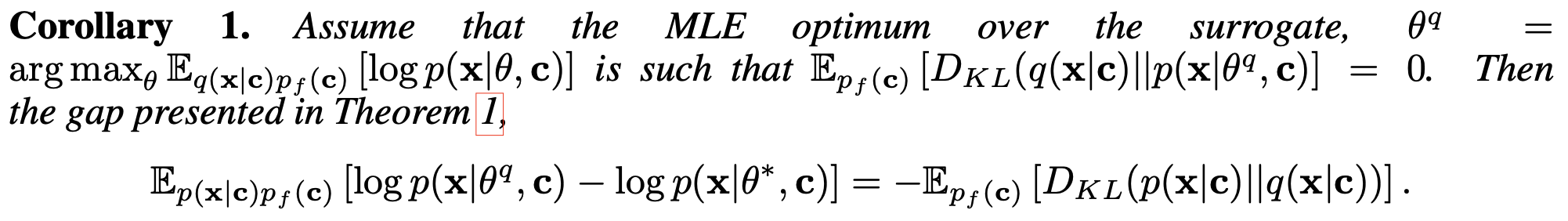
Corollary 1은 $q(\mathbf{x} \vert \mathbf{c}_f)$와 $p(\mathbf{x} \vert \mathbf{c}_f)$사이의 차이가 클수록 얻을수 있는 $D_f$에 대한 log-likelihood는 낮아진다는 것을 보인다. 여기서 $q(\mathbf{x} \vert \mathbf{c}_f) \neq p(\mathbf{x} \vert \mathbf{c}_f)$여야 하므로, $q(\mathbf{x} \vert \mathbf{c}_f)$를 아무 분포나 자유롭게 골라도 된다.
최종적인 Selective Amnesia(SA) objective는 다음과 같다.

여기서 likelihood term을 각각의 evidence lower bound로 대체한다. Variational model들에 대해, ELBO를 최대화하는 것은 likelihood를 증가시키고 본 논문은 위 objective가 더 좋은 결과를 보이는 것을 보인다.
2. Experiments
2.1 MNIST, CIFAR10 and STL10 Results

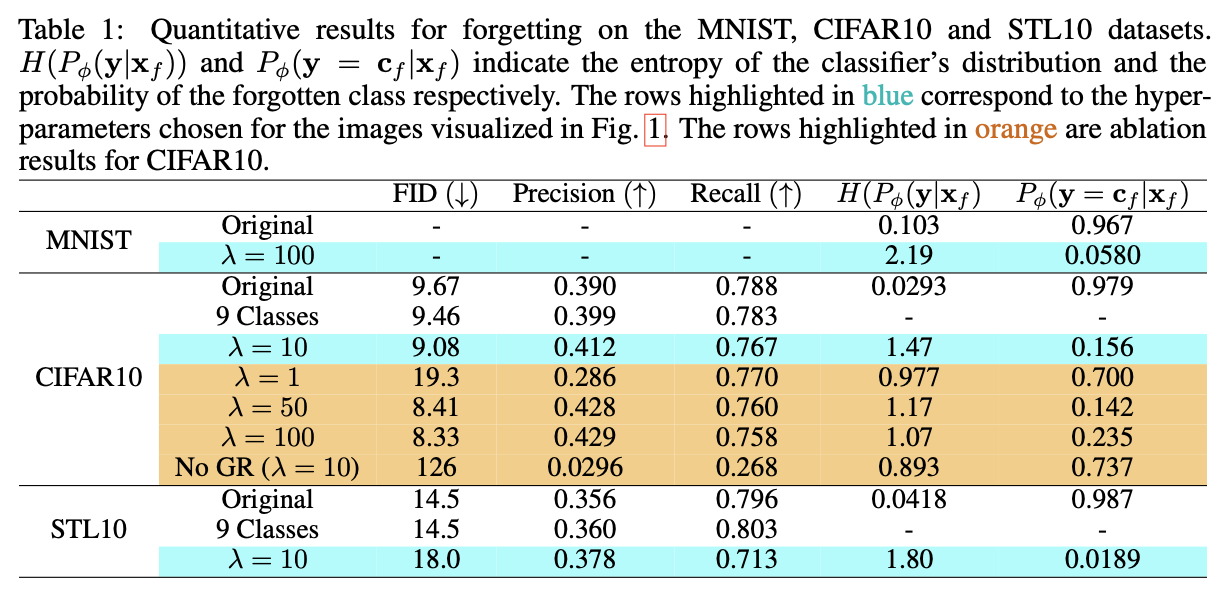
2.2 Case Study : Stable Diffusion
Forget Famous Persons
SD를 이용한 실험에서 "Brad Pitt"나 "Angelina Jolie"를 지우고 싶을 때, "a middle aged man"이나 "a middle aged woman"와 같은 prompt로 생성한 이미지들로 $q(\mathbf{x} \vert \mathbf{c}_f)$를 나타낸다.


Forget Nudity

3. Limitations
- FIM 계산이 엄청나다
- SA는 'global' concept을 지우는 것보단 'local' specific concept을 지우는 것에 더 유용
- 적절한 surrogate distribution에 대한 maual selection이 필요
Take Away
- Continual Learning을 이용했다곤 하지만 Continual하게 새로운 concept을 지우는 것을 학습하는 느낌이 아닌 것 같다... 그런 실험이 존재 하지 않는듯...
- Objective term은 그래도 이해해두면 도움이 될지도?




