| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- flow models
- Programmers
- unlearning
- inversion
- ddim inversion
- Concept Erasure
- rectified flow models
- 3d generation
- rectified flow matching models
- rectified flow
- 논문리뷰
- 네이버 부스트캠프 ai tech 6기
- diffusion model
- memorization
- 코테
- Python
- 프로그래머스
- video generation
- 3d editing
- VirtualTryON
- flow matching
- visiontransformer
- diffusion
- image generation
- image editing
- diffusion models
- flow matching models
- video editing
- Machine Unlearning
- BOJ
- Today
- Total
평범한 필기장
[평범한 대학원생이 하는 논문 간단 요약] How to Continually Adapt Text-to-Image Diffusion Models for Flexible Customization? (NeurIPS 2024) 본문
[평범한 대학원생이 하는 논문 간단 요약] How to Continually Adapt Text-to-Image Diffusion Models for Flexible Customization? (NeurIPS 2024)
junseok-rh 2025. 9. 12. 22:15Paper : https://arxiv.org/abs/2410.17594
How to Continually Adapt Text-to-Image Diffusion Models for Flexible Customization?
Custom diffusion models (CDMs) have attracted widespread attention due to their astonishing generative ability for personalized concepts. However, most existing CDMs unreasonably assume that personalized concepts are fixed and cannot change over time. More
arxiv.org
Abstract
기존 continual diffusion models의 문제점은 새로운 concept을 학습하면 기존 오래된 concept을 무시하거나 잊어버리는 것이다. 본 논문은 이를 해결할 새로운 방식인 Concept-Incremental text-to-image Diffusion Models(CIDM)을 제안한다.
0. Problem Definition

1. The Proposed Model
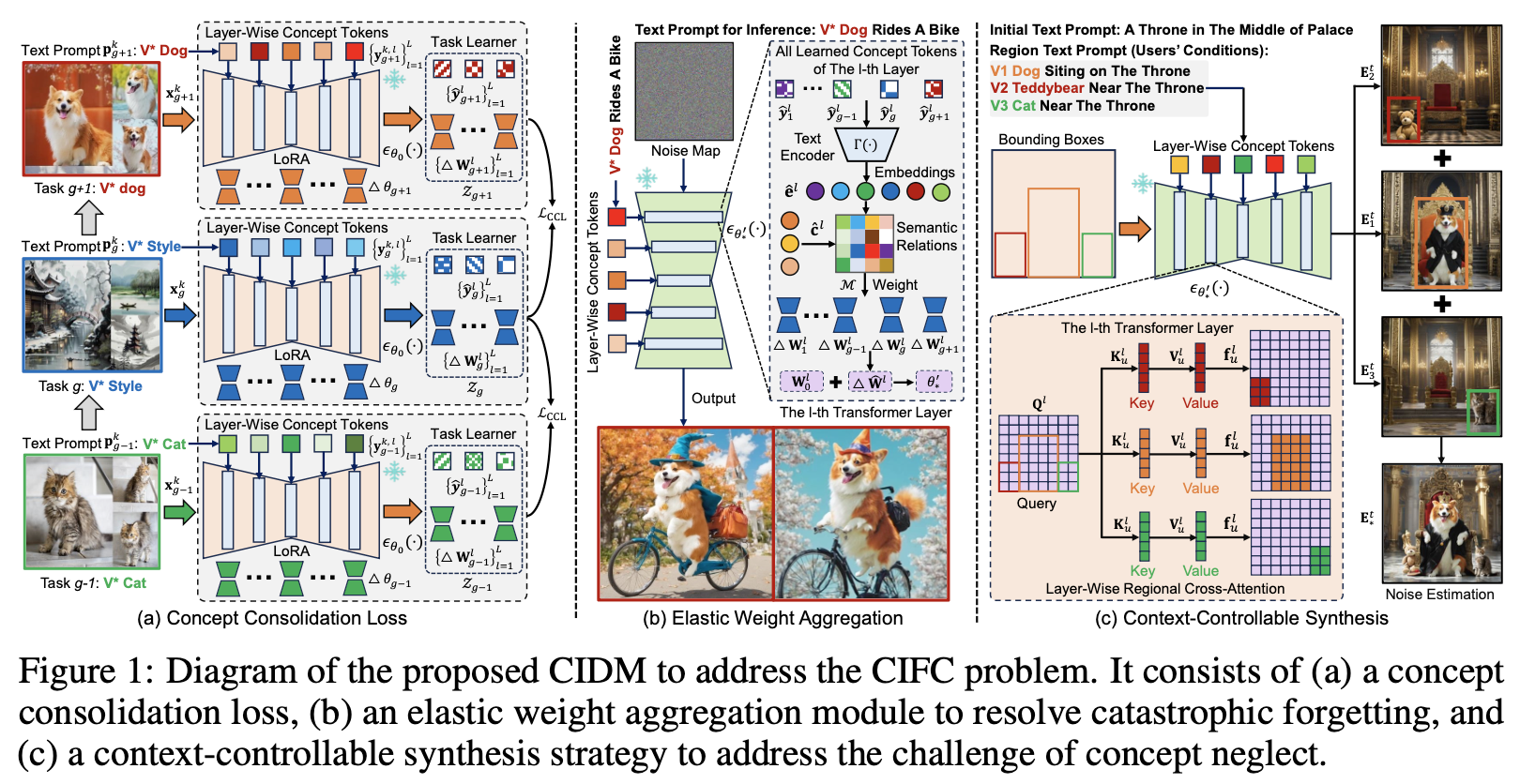
1.1 Concept Consolidation Loss
$g$번째 text-guided concept customization task $\mathcal{T}_g$를 학습하기 위해서, (1)을 최적화 함으로써 personalized data $\{ \mathbf{x}^k_g, \mathbf{p}^k_g, \mathbf{y}^k_g \}^{n_g}_{k=1}$에 대해서 UNet $\epsilon_{\theta_0}(\cdot)$ 을 LoRA를 사용해서 finetuning한다.
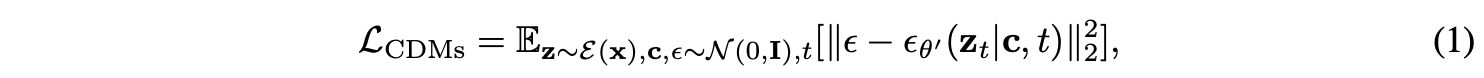
이를 통해서 updated model $\epsilon_{\theta^\prime_0}(\cdot)$을 얻는다. 여기서 $\epsilon^\prime_g = \epsilon_0 + \triangle\theta_g$이고 $\triangle \theta_g = \{ \triangle \mathbf{W}^l_g \}^L_{l=1}$이다. $\triangle \mathbf{W}^l_g = \mathbf{A}^l_g \mathbf{B}^l_g \in \mathbb{R}^{a \times b}$이다. $\triangle \theta_g$는 $g$번째 task안에 있는 personalized concept identity를 대부분 encoding할 수 있다. 가장 단순한 방식은 모든 task의 LoRA weight를 저장하고, linear하게 그들을 merge하는 것이다. 하지만 이 방식은 continual하게 새로운 concept을 학습할 때, 몇몇 personalized concept들의 개개인 특징들의 상당한 loss를 발생시킨다 (catastrophic forgetting). 이를 완화하기 위해서 본 논문은 concept consolidation loss $\mathcal{L}_{CCL}$을 제안한다.
Task-Specific Knowledge
Task-Specific Knowledge는 각 concept customization task 안에 personalized concepts의 구별되는 특징을 나타낸다. 이 특징을 찾기 위해서, 본 논문은 합성된 이미지안에 personalized concept들의 unique attribute들을 더 잘 보존하기 위해 learable layer-wise concept token들을 도입한다 (기존에 모든 layer에 unified token을 넣는 textual inversion 방식과 다름). Image $\mathbf{x}^k_g$의 textual description $\mathbf{p}^k_g$ (photo of a $[ V_* ] [ V_{dog} ]$)가 주어지면, $l$번째 layer의 text prompt를 $\mathbf{p}^{k,l}_g$ (photo of a $[ V_*^l ] [ V_{dog}^l ]$)로 정의하고 $[ V_*^l ] [ V_{dog}^l ]$는 $l$ layer에서의 learnable concept tokens $\mathbf{y}^{k,l}_g$를 나타낸다. 본 논문은 textual embedding $\mathbf{c}^{k,l}_g = \Gamma(\mathbf{p}^{k,l}_g)$을 $\epsilon_{\theta^\prime_g}(\cdot)$의 $l$번째 layer에 넣는다. 수식 (1)을 통해 $\epsilon_{\theta^\prime_g}(\cdot)$을 학습할 때, learnable layer-wise concept token은 catastrophic forgetting을 해결하기 위해서 다른 layer들로부터 old personalized concept들의 유니크한 컨셉을 캡쳐할 수 있다.
Concept customization task의 수가 증가하면 다른 personalized concept들을 구별하는 task-specific knowledge의 discriminative 능력이 악화된다. 본 논문은 이를 해결하기 위해서 다른 customization task의 low-rank weight를 제한하는 orthogonal subspace regularizer를 고안한다. 이는 다른 테스크에 따른 concept subspace의 orthogonality를 보장함으로써 task-specific knowledge의 discriminative 능력을 강화한다. 다른 테스크들의 low-rank concept subspace들에 대한 orthogonal subspace regularizer는 $\Sigma^{g-1}_{i=1} \Sigma^{L}_{l=1} \mathbf{A}^l_i (\mathbf{A}^l_g)^\top = 0$로 수행한다. 이는 미분이 불가능하기 때문에, $\mathcal{R}_1 = \Sigma^{g-1}_{i=1} \Sigma^{L}_{l=1} \mathbf{A}^l_i (\mathbf{A}^l_g)^\top$을 최소화하는 alternative optimization strategy를 제안한다.
Task-Shared Knowledge
Task-shared knowledge는 의미적으로 유사한 컨셉들을 가진 다른 테스크들 사이에 공유되는 semantic 정보를 나타낸다. 이는 old personalized concept들에 대한 catastrophic forgetting을 다루는데 효과적이다. Task-shared knowledge를 캡쳐하기 위해서, 본 논문은 $l$ layer에서 다른 테스크에 대해 공유되는 layer-wise common subspace $\mathbf{W}^l_* \in \mathbb{R}^{a \times b}$를 제안한다. 이전에 학습한 low-rank weights $\{ \triangle \theta_i \}^g_{i=1}$이 주어지면, learnable projection matrix $\mathbf{H}^l_i \in \mathbb{R}^{a \times a}$가 $\mathcal{R}_2 = \sum_{i=1}^g \sum_{l=1}^L \left\| \triangle \mathbf{W}^l_i - \mathbf{H}^l_i \mathbf{W}^{l}_* \right\|_F^2$를 통해 $\{\triangle \theta_i\}_{i=1}^g$의 common semantic information을 $\mathbf{W}^{l}_*$에 encoding할 수 있다.
$g$ 테스크에 대해서, task-specific과 task-shared knowledge를 동시에 학습하기 위한 concep consolidation loss $\mathcal{L}_{CCL}$은 다음과 같다.

Two-Step Optimization
먼저 task-specific information을 캡쳐하기 위해, (2)를 이용해서 $\mathbf{H}^l_i$와 $\mathbf{W}^l_*$를 고정하고 learable layer-wise concept token들과 low-rank weight $\triangle \theta_g = \{ \mathbf{W}^l_g \}^L_{l=1}$를 update한다. 그러고 나서, task-shared knowledge를 찾기 위해, $\triangle \theta_g$와 learnable layer-wise concept token들을 고정하고 (2)에서 $\mathcal{R}_2$를 통해서 $\mathbf{H}^l_i$와 $\mathbf{W}^l_*$를 update한다. $g$번째 concept customization task를 학습하고 나서, 본 논문은 task learner $\mathcal{Z}_g = \{ \triangle \mathbf{W}^l_g, \mathbf{\hat{y}}^l_g \}^L_{l=1}$를 얻는다.
1.2 Elastic Weight Aggregation
Inference 동안 old personalized concepts에 대한 catastrophic forgetting을 다루기 위해서, 본 논문은 이전에 학습된 $g$개의 task learner $\{ \mathcal{Z}_i \}^g_{i=1}$를 저장(memory storage 0.25%)하고, 그들을 merge하기 위해서 elastic weight aggregation (EWA) module을 제안한다. Text prompt $\hat{\mathbf{p}}$이 주어지면, 이를 통해 textual embedding $\hat{\mathbf{c}}$을 뽑는다. 또한 stoked task learner에서 모든 concept token들을 각각 text encoder를 통해서 encoding을 하고 같은 task에 속하는 embedding은 평균내서 새로운 embedding $\hat{\mathbf{e}}$를 얻는다. 그 후에, $\hat{\mathbf{c}}^l$와 $\hat{\mathbf{e}}^l$사이의 semantic relations $\mathcal{M}$을 계산하고 이를 통해 $l$ layer안의 모든 학습된 테스크의 low-rank weights $\{ \triangle \mathbf{W}^l_i \}^g_{i=1}$를 adaptivley merge한다. Merged low-rank weights $\triangle \hat{\mathbf{W}}^l$은 다음과 같이 계산된다.

$\text{max}(\cdot)$은 row axis에 따라 maximization function을 나타내고 $\psi(\mathcal{M}) = \mathcal{M}^2 / \Vert \mathcal{M}^2 \Vert_F$이다.
Inference
(3)을 이용해서 기존에 학습된 모든 low-rank weights를 merge하고 나서, 새로운 denoising UNet $\epsilon_{\theta^\prime_*}(\cdot)$을 얻는다. $\theta^\prime_*$는 모든 이전에 학습된 personalized concept들의 상당한 구별되는 attribute들을 encoding해, inference동안 old concept들의 catastrophic forgetting을 효과적으로 완화한다.
1.3 Context-Controllable Synthesis
위에서 얻은 $\epsilon_{\theta^\prime_*}(\cdot)$를 사용하면 concept neglect문제가 발생한다. 그래서 본 논문에서는 context-controllable synthesis strategy를 제안한다.
Conditional Generation
$U$개의 Region condition $\{ \hat{\mathbf{p}}_u, \hat{\mathbf{s}}_u \}^U_{u=1}$가 제공됐을 때를 가정한다. 여기서 $\hat{\mathbf{s}}_u$는 $u$번째 region text prompt $\hat{\mathbf{p}}_u$와 연관된 concept을 합성할 bounding box이다. $\Gamma(\cdot)$를 통해 $\hat{\mathbf{p}}_u$에 대한 layer-wise textual embedding $\hat{\mathbf{c}}_u$를 뽑는다. 일반적인 denoising process를 통해 $l$번째 transformer layer에서의 feature map $\mathbf{f}^l$을 구할 수 있다. 그리고 $\hat{\mathbf{c}}^l_u$와 $\mathbf{f}^l$사이의 layer-wise regional cross-attention $\mathbf{f}^l_u = \sigma (\mathbf{Q}^l (\mathbf{K}^l_u)^\top / \sqrt{d}) \cdot \mathbf{V}^l_u$을 수행해서 $u$번째 region feature $\mathbf{f}^l_u$를 얻을 수 있다. ($\mathbf{Q}^l = \Omega(\mathbf{f}^l\mathbf{w}_q \odot \hat{\mathbf{m}^l_u}), \ \mathbf{K}^l_u = \hat{\mathbf{c}}^l_u\mathbf{w}_k, \ \mathbf{V}^l_u = \hat{c}^l_u \mathbf{w}_v$) $\hat{\mathbf{m}}^l_u$는 $l$ layer에서 binary retgion mask이다. 이는 bounding box $\hat{\mathbf{s}}_u$안의 값들은 1로 설정된다. $\Omega(\cdot)$은 $\hat{\mathbf{s}}_u$안의 feature들만 유지한다. Bounding box내의 $\mathbf{f}^l$ 값들은 각각 대응되는 region feature $\mathbf{f}^l_u$의 값들로 대체돼고 이를 통해 최종적인 new feature map $\hat{\mathbf{f}}^l$을 얻는다. 본 논문은 모든 layer들에 대해 layer-wise regional cross-attention을 적용한다.
Multi-Concept Composition
위를 통해 얻은 denoising UNet $\epsilon_{\theta^\prime_*}(\cdot)$을 가지고 initial text prompt $\hat{\mathbf{p}}$에 대한 noise estimation $\mathbf{E}^t = \epsilon_{\theta^\prime_*}(\mathbf{z}_t \vert t) + s \cdot (\epsilon_{\theta^\prime_*}(\mathbf{z}_t \vert \hat{\mathbf{c}},t) - \epsilon_{\theta^\prime_*}(\mathbf{z}_t \vert t))$을 얻을 수 있다. $u$번째 region condition에 대한 noise estimation $\mathbf{E}^t_u$를 다음과 같이 구할 수 있다.

Multi-concept customization에 대해서, concept neglect을 해결하기 위해서 $U$개의 region noise estimation을 다음과 같이 모은다.

최종적으로 image를 생성하기 위해서 $\mathbf{E}^t_*$를 보낸다.

Take Away
매서드가 상당히 복잡하게 많게 느껴졌지만, 그래도 내가 챙겨가야할 부분은 많지 않았던 것 같다. 실험과 appendix 내용은 따로 정리하지 않을 예정이다.
- 이 포스트에는 없지만 본 논문에서 multi-concept customization benchmark dataset을 만들었는데, 이 데이터셋은 내 연구에 필요해 보였다. 혹은 이 데이터셋을 만드는 방식 정도?
- Concept Consolidation Loss와 Elastic Weight Aggregation은 내 연구에서 적용할만 할 것 같다.




