| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 3d editing
- video editing
- 3d generation
- visiontransformer
- BOJ
- Vit
- VirtualTryON
- transformer
- DP
- segmenation map generation
- flipd
- 코테
- 코딩테스트
- segmentation map
- masactrl
- 프로그래머스
- noise optimization
- memorization
- diffusion models
- 논문리뷰
- image editing
- inversion
- diffusion
- 네이버 부스트캠프 ai tech 6기
- video generation
- Python
- flow matching
- Programmers
- diffusion model
- rectified flow
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] Unveil Inversion and Invariance in Flow Transformer for Versatile Image Editing (CVPR 2025) 본문
[평범한 학부생이 하는 논문 리뷰] Unveil Inversion and Invariance in Flow Transformer for Versatile Image Editing (CVPR 2025)
junseok-rh 2025. 4. 13. 18:47Paper : https://arxiv.org/abs/2411.15843
Unveil Inversion and Invariance in Flow Transformer for Versatile Image Editing
Leveraging the large generative prior of the flow transformer for tuning-free image editing requires authentic inversion to project the image into the model's domain and a flexible invariance control mechanism to preserve non-target contents. However, the
arxiv.org
1. Introduction
Flow transformer의 editing challenge는 inversion for flow와 invariance control based on the flow transformer라는 두 가지 major 이슈로부터 온다. 본 논문에서는 이러한 두 가지 문제를 해결하는 것을 목표로 한다.

2. Inversion for Rectified Flow
Rectified Flow에서 정확한 Euler inversion은 (7)이다. 그러나, $\mathbf{x}_t$가 아닌 $\mathbf{x}_{t+1}$만 알기에, (8)처럼 $\mathbf{x}_{t+1}$를 이용해서 $\mathbf{x}_t$를 approximate한다. 이는 매 스탭마다 approximation error를 가져오고 이는 쌓여서 initial latent $\mathbf{x}_0$로부터 멀어진다.
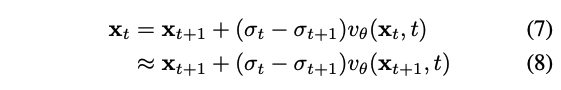
2.1 Deficiency and Relation of Euler to DDIM

$\mathbf{x}_t$를 $\frac{\mathbf{x}_t}{\sqrt{\alpha_t}}$로 rescale하고 (5)를 다시 쓰면, DDIM은 first-order ODE solver로 여겨질 수 있다. 이에 대응되는 inversion은 다음과 같다.

Euler와 DDIM inversion의 유사한 formulation에도 불구하고, Euler inversion의 performance는 DDIM inversion에 비해 상당히 떨어진다.

본 논문은 이는 rectified flow transformer를 위한 Euler inversion은 approximation error에 대해 더 민감하기 때문이라고 주장한다. 이를 줄이기 위해, $v_\theta(\mathbf{x}_{t+1},t)$와 $v_\theta(\mathbf{x}_t,t)$사이의 gap을 완화할 필요가 있다.
2.2 Two-stage Flow Inversion
본 논문의 목표는 가능한 진짜 generation process와 가까운 initial latent와 inversion trajectory를 찾는 것이다. 이는 Editing Friendly하고 Easy to preserve invariance and fidelity라는 이점을 가진다. 이를 위해서 본 논문은 two-stage flow inversion을 제안한다. 먼저 generating process에 가까운 pivotal inversion을 구성한다. 다음으로 각 timestep마다 compensate를 더해 남은 mild error를 없앤다.
Stage I : Fixed point iteration with stable velocity.
Approximation없이 정확한 $\mathbf{x}_t$를 얻기 위해서 (7)을 사용하는 것을 목표로 한다. 이를 위해서, $v_\theta(\mathbf{x}_t,t)$의 estimation을 향상시킬 필요가 있다. $v_\theta(\mathbf{x}_t,t)$의 input과 (7)의 output이 모두 $\mathbf{x}_t$이다. Fixed-point technique에 영감을 받아, 반복적으로 $\mathbf{x}_t$를 (7)적용할 수 있고 이를 통해 $v_\theta(\mathbf{x}_t,t)$를 더 잘 추정할 수 있다. 구체적으로, $\mathbf{x}_{t+1}$로 $\mathbf{x}^1_t$를 초기화하고 반복적으로 다음 equation을 적용해서 series of estimation $\{ \mathbf{x}^i_t \}^I_{i=1}$을 얻고 이들을 average한다.


Stage II : Velocity compensation in editing.
Fixed-point iteration은 수치적인 방식이기 때문에, inverted $\mathbf{x}_0$로부터 $\mathbf{x}_1$을 recover할 때 여전히 error가 존재한다. Inversion trajectory $\{ \mathbf{x}_t \}^T_{t=1}$로 original image $\mathbf{x}_1$를 정확히 recover하기 위해서, 매 time step때, generation process(editing process) 동안 velocity를 위한 compensation $\epsilon_t$을 계산하고 더해준다.

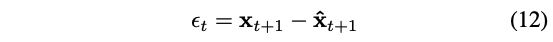


3. Flexible Invariance Control with AdaLN
본 논문의 key observation은 AdaLN(Adaptive Layer Normalization)안의 text feature들은 image semantics에 대응된다는 것이다. AdaLN의 before와 after text feature를 $M^a, M^b \in \mathbb{R}^{j \times d}$로 나타낸다. 본 논문은 before prompt $\mathcal{P}_b$에서 token들과 대응되는 after prompt $\mathcal{P}_a$에서 unedited tokens의 feature를로 바꾸는 token aware Map function $\mathbf{Map}(M^b,M^a,\mathcal{P}_b,\mathcal{P}_a)$를 정의한다.

본 논문은 다양한 시나리오에서 잠재력을 보여준다.

이 결과는 AdaLN에서 대체된 text feature $\hat{M}^a$은 다른 editing 시나리오에 적응한다는 것을 보인다. 또한 본 논문은 Self-Attention에 대한 조사한다.

너무 많은 timestep에서의 attention injection은 non-rigid editing effect를 막는다. 다른 방식과 대조적으로 본 논문은 모든 editing type에 대해서 injection timestep $S$를 동일하게 설정한다.
4. Experiments
4.1 Comparison with previous editing methods


4.2 Ablation Study and Analysis
Number of fixed-point iterations


Velocity compensation
Figure 9를 보면 left error는 크지 않고 veolcity compensation은 정확한 original image를 recover할 수 잇고 editing의 fidelity를 향상시킬 수 있다.
Limitation
만약 real image가 model의 domain 밖에 존재하고 inversion이 generation process에 너무 벗어나면, inversion이 model의 prior 분포와 fit하지 않고 text-to-image alignment가 mismatch됐기 때문에 module은 정확히 content를 control할 수 없다. Fixed-point iteration의 computational efficiency도 한계점이다.





