| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- VirtualTryON
- Machine Unlearning
- flow matching models
- 논문리뷰
- BOJ
- rectified flow
- visiontransformer
- diffusion
- ddim inversion
- image generation
- flow models
- 네이버 부스트캠프 ai tech 6기
- image editing
- 3d editing
- unlearning
- 프로그래머스
- rectified flow matching models
- diffusion models
- memorization
- 코테
- rectified flow models
- Programmers
- video generation
- 3d generation
- video editing
- inversion
- diffusion model
- Python
- Concept Erasure
- flow matching
- Today
- Total
평범한 필기장
[평범한 대학원생이 하는 논문 간단 요약] FlowEdit: Inversion-Free Text-Based Editing Using Pre-Trained Flow Models (ICCV 2025 Oral) 본문
[평범한 대학원생이 하는 논문 간단 요약] FlowEdit: Inversion-Free Text-Based Editing Using Pre-Trained Flow Models (ICCV 2025 Oral)
junseok-rh 2025. 10. 5. 22:23Paper : https://arxiv.org/abs/2412.08629
FlowEdit: Inversion-Free Text-Based Editing Using Pre-Trained Flow Models
Editing real images using a pre-trained text-to-image (T2I) diffusion/flow model often involves inverting the image into its corresponding noise map. However, inversion by itself is typically insufficient for obtaining satisfactory results, and therefore m
arxiv.org
Abstract
기존 T2I model들을 이용한 real image editing은 image를 대응되는 noise map으로 inverse하는 inversion 과정을 필요로 했다. 이러한 inversion 과정만으로는 만족스러운 결과물을 얻을 수 없었다. 그래서 이를 해결하기 위해서 sampling 과정에서 추가적인 개입을 필요로 한다. 하지만 이런 방식들은 model architecture에 대해서 자연스러운 전환이 어렵다.
본 논문은 그래서 inversion-free이고, optimization-free이면서, model agnostic한 editing method인 FlowEdit을 제안한다.


1. Reinterpretation of editing by inversion

Inversion based editing은 Gaussian noise의 분포를 통과하면서 source에서 target 분포로 이동하는 방식이다. 이는 근데 source 분포에서 target 분포로 직접 이동하는 것으로 표현될 수 있다.
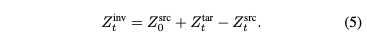
위 이미지에서 회색 평행사변형이 (5)의 관계를 나타낸다. (3)와 (4)를 이용해서 (5)를 ODE로 나타내면 (6)과 같다.
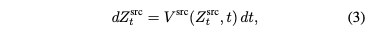

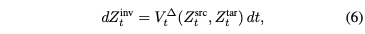
여기서 $V^\Delta_t(Z^{src}_t, Z^{tar}_t) = V^{tar}(Z^{tar}_t, t) - V^{src}(Z^{src}_t,t)$이다. (5)를 이용해서 (6)을 바꾸면, direct path가 다음 ODE의 solution인 것을 볼 수 있다.

(7)을 통한 path가 특별한 이유는 이 path를 따르는 이미지들은 noise-free라는 것이다. 이러한 이유는 noisy image $Z^{tar}_t, Z^{src}_t$가 rough하게 동일한 noise 구성요소를 보유하기 때문이다. 그러므로, $V^{tar}(Z^{tar}_t,t), V^{src}(Z^{src}_t,t)$가 rough하게 동일한 noise component를 지우고, 이는 clean image prediction들 사이의 차이만 포함한다.
$t$가 1에 가까울 때, $Z^{src}_t, Z^{tar}_t$의 noise level이 커서 $V^\Delta_t(Z^{scr}_t, Z^{tar}_t)$가 coarse image structure에 대한 차이만 capture한다. $t$가 작아질수록, noise level은 감소하고 higher frequency content들이 나타난다. 즉, (7)은 일종의 $Z^{src}_0$에서 $Z^{tar}_0$로의 autoregressive coarse-to-fine evolution를 구성한다.
Editing-by-inversion 방식을 위와 같이 재해석할 수 있는데, 이 재해석이 본 논문의 method의 motivation이 됐다.
2. FlowEdit
Editing-by-inversion이 direct ODEf로 표현될 수 있다는 사실이 source와 target sample들 사이의 바람직한 pairing을 야기한다는 것을 내포하지 않는다. 본 논문에서는 source와 target 분포가 중심이 $\{ ( -\frac{15}{\sqrt{2}},-\frac{15}{\sqrt{2}} ), ( \frac{15}{\sqrt{2}},\frac{15}{\sqrt{2}} ) \}, \{ (-15, 0), (0,15) \}$인 gaussian mixture를 이용한 실험을 진행한다.

Editing의 관점에서, source 분포는 가장 가까운 target 분포로 이동해야한다. 하지만, inversion을 이용한 editing 방식에서는 오른쪽 아래의 결과가 나타났다. 이는 초기 Gaussian noise로 어떻게 매핑이 되는가에 따라 target 분포로 매핑이 된다.
본 논문의 목표는 source와 target sample들 사이의 거리가 더 낮은 거리를 야기하는 alternative mapping을 구성하는 것이다. 본 논문의 방식인 FlowEdit은 오른쪽 위 이미지와 같이, source 분포가 target 분포의 가장 가까운 mode로 매핑시킨다. FlowEdit의 매핑 방식은 target 분포로 정확하게 매핑하는 것을 보장하지는 않지만, target text prompt를 잘 반영하면서 SOTA의 structure preservation을 보인다.

본 논문의 key idea는 여러 개의 random pairing을 사용해, 연관된 velocity field들을 평균내는 것이다. 구체적으로, (7)과 동일한 ODE를 제안하지만, 동일한 marginal을 지닌 다른 random process로 inversion path $Z^{inv}_t$를 대체한다. 다음과 같은 대안의 forward process를 고려해보자.

여기서 $N_t$은 $Z^{src}_0$와 통계적으로 독립이고 모든 $t \in [0,1]$에 대해서 $N_t \sim \mathcal{N}(0,I)$인 marginal을 가지는 gaussian process이다. 다음 ODE를 풂으로써 path $Z^{FE}_t$를 구성한다.

(9)가 process $\hat{Z}^{src}_t$의 marginal에 대해서만 depend하고 전체 분포에는 depend하지 않기 때문에 $N_t$의 covariance function을 특정할 필요는 없다.
(8)을 통해서 $\hat{Z}^{src}_t$의 분포를 구한다. 그리고 $\hat{Z}^{tar}_t = Z^{FE}_t + \hat{Z}^{src}_t - Z^{src}_0$를 계산해서 얻은 $\hat{Z}^{tar}_t$과 $\hat{Z}^{src}_t$를 가지고 velocity field $V^\Delta_t(\hat{Z}^{scr}_t, \hat{Z}^{tar}_t) = V^{tar}(\hat{Z}^{tar}_t,t) - V^{src}(\hat{Z}^{src}_t,t)$를 계산한다. 이 과정을 여러 번 반복하고 이들을 평균내서 최종 update direction을 얻는다.

2.1 Practical considerations
(9)의 기댓값은 각 timestep마다 $n_{avg}$개의 model prediction들의 평균으로 근사된다. 이론과 달리, $n_{avg}$가 작을 때 $N_t$의 covariance function이 영향을 끼친다. 그래서 좋은 근사를 얻기 위해서, 본 논문은 $\mathbb{E}[ N_t, N_s] = 0$을 만족하는 $N_t$의 covariance function을 골라, timestep에 따라 noise가 independent하게 되도록 한다.
(9)의 averaged velocity term은 difference $\mathbb{E}\!\left[ V_{\text{tar}}(Z^{\text{tar}}_t, t) \,\middle|\, Z^{\text{src}}_0 \right] - \mathbb{E}\!\left[ V_{\text{src}}(Z^{\text{src}}_t, t) \,\middle|\, Z^{\text{src}}_0 \right]$와 대응되는데, 이는 $\hat{Z}^{tar}_t, \hat{Z}^{src}_t$를 독립적으로 샘플링함으로써 계산할 수 있다. 그러나 본 논문은 이 들을 같은 noise instance로 계산해 작은 $n_{avg}$ 값에 대한 robustness를 향상시킨다.
또한, 기존 inversion 방식에서의 적용한 것과 동일하게 모든 timestep에 대해서 계산하지 않고 특정 timestep 기준을 정해둬서 timestep 이후에만 계산하도록 하는 방식을 적용한다.
2.2 Comparison to editing by (exact) inversion

FlowEdit과 inversion 방식을 이용해서 cat을 dog으로 바꾸는 실험을 간단하게 진행했다. Source image드과 target image들의 latent space상의 MSE와 decoding된 이미지들의 LPIPS를 계산해서 transport cost를 측정했고, SD3으로 생성한 이미지들과의 FID와 KID 비교를 통해서 target 분포와의 alignment도 측정했다. FlowEdit이 lower transport cost (1376 vs. 2239 for MSE, 0.15 vs. 0.25 for LPIPS)와 lower FID (51.14 vs. 55.88), KID (0.017 vs. 0.023)를 보였다.
3. Experiments
Baseline Models : Flux.1 dev, SD3 Medium
3.1 Qualitative Results


3.2 Quantitative Results
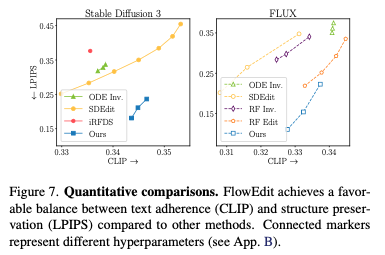
3.3 Text-based style editing

4. Limitations
FlowEdit의 장점이 강한 structure preservation인데, 이 때문에 이미지에서 큰 부분에 대한 큰 변경이 필요할 때 잘 안된다. (배경이나 포즈)

TakeAway
- Inversion 과정을 source 분포에서 target 분포로 바로 보내는 것으로 해석할 수 있다.
- 위 아이디어를 통해, editing을 source분포에서 target 분포로 보내는 ODE로 나타낼 수 있고 이 ODE를 풂으로써 editing을 inversion없이 할 수 있다.




