[평범한 학부생이 하는 논문 리뷰] Attention is all you need (Transformer)

Transformer 자체는 이 전에 CS231n으로 대충 공부는 해봤지만 그래도 중요한 논문이기에 논문 자체를 읽어봐야겠다는 생각을 했었다. 이번 방학 때 시간이 되어 논문을 읽어보고 블로그에도 정리해보는 시간을 가졌다. 이번 논문 리뷰는 나동빈님의 논문 리뷰영상과 자료를 많이 참고해서 작성했다.

https://arxiv.org/abs/1706.03762

Attention Is All You Need

1. Abstract

기존의 sequence transduction 모델들과 달리 이 논문에서 제안한 Transformer라는 모델은 reccurency와 convolution을 완전히 배제하고 attention 메커니즘만을 기반으로 한다. 실험을 해본 결과 품질이 우수하고 병렬화가 가능하면서 훈련에 훨씬 적은 시간이 소요된다고 한다.

2. Introduction

기존의 Recurrent Model (RNN, LSTM, GRU 등등)은 순차적인 특성을 지닌다. 즉 $h_{t-1},\ t$의 함수 $h_t$를 생성하는 형태를 말한다. 본질적인 순차적 특성은 메모리 제약으로 인해 예제 간 일괄 처리가 제한되므로 훈련 예제 내에서 병렬화를 막는다. 그런데 병렬화는 시퀀스 길이가 길어질수록 중요하다. 즉, 긴 input에 대한 기존 모델들의 한계점이 드러난다.

 

Attention은 입력 또는 출력 시퀀스의 거리에 관계없이 종속성을 모델링할 수 있게 해준다. 기존의 모델들은 attention와 recurrent network를 같이 사용했지만, 이 논문에서 제안한 Transformer는 기존의 모델들과 달리 Attention에만 의존하는 모델이라고 설명한다.

 

특히, 트랜스포머는 기존의 Attention 매커니즘을 이용하는 것이 아닌 Self-Attention 매커니즘을 이용한다. Attention과 Self-Attention의 차이는 다음에 기회가 되면 비교해가며 설명하겠다.

3. Model Architecture

Transformer의 Architecture

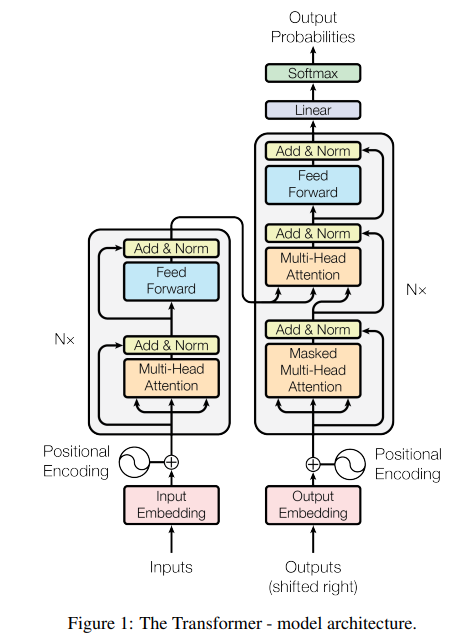
위 이미지는 Transformer의 전체 architecture를 나타낸다. 위 이미지를 보면 self-attention과 point-wise fully connected layers로 구성된 것을 볼 수 있다. 위 이미지에서 왼쪽이 encoder, 오른쪽이 decoder를 나타낸다. 

3.1 Positional Embedding

Transformer의 구조를 보면 input이 들어오면 임베딩 과정을 거치는데 이러한 임베딩에는 위치 정보가 들어있지 않다. 기존의 RNN과 같은 Sequence Model은 input이 들어오는 순서대로 처리하기 때문에 위치 정보를 따로 다룰 필요가 없었다. 하지만 Transformer는 들어오는 Input을 한번에 처리하기 때문에 위치 정보를 따로 지정해줄 필요가 있다. 그렇기 때문에 Positional Encoding을 도입했다. 

Positional Encoding은 아래와 같은 주기함수를 이용해 각 임베딩 벡터에 위치 정보를 넣어준 것이다.

$$P E_{(pos,2i)} = sin(pos/10000^{2i/d_{model}})$$

$$P E_{(pos,2i+1)} = cos(pos/10000^{2i/d_{model}})$$

출처 : https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

이렇게 함으로써 RNN과 같은 Sequence model을 이용하지 않고 각 단어에 위치 정보를 넣어줄 수 있다.

3.2 Attention

출처 : https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

위의 이미지는 Encoder를 나타낸 그림이다. Encoder의 각 layer는 동일한 형태를 지닌다. 그리고 논문에서는 6개의 layer로 쌓는다고 말한다. 하나의 layer를 자세히 보면 embedding 과정이 수행된 input이 들어오면 residual learning방식으로 multi-head attention을 수행하고 그 결과와 input을 더하고 normalization을 수행하고 동일한 방식으로 feedforward layer를 지난다. 여기서 각 레이어마다 다른 파라미터를 가진다.

 

3.2.1 Self Attention

Multi-head attention을 자세하게 뜯어보자.

왼 : Scaled dot-product attiontion, 오 : Multi-head attention

위 이미지를 통해 Attention의 작동 원리를 이해기 전에 이미지에 있는 Q(Query), K(Key), V(Value)를 먼저 이해해야 한다. 'l love you'라는 문장을 예로 들면 우리는 'I'라는 단어를 기준으로 이 문장에 있는 단어와 얼마나 관련있는지를 계산하고 싶어한다. 이 때, 'I'를 query라 하고 문장 내 모든 단어를 key라 한다. 

출처 : https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

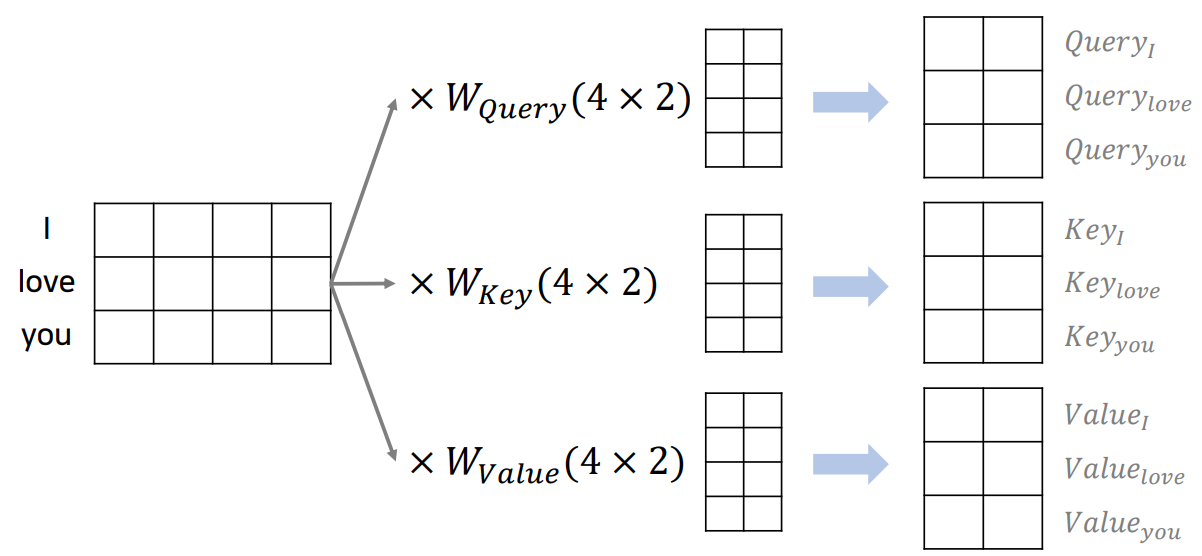
Attention값을 구하기 위해서 우리는 query, key, value 값을 알아야한다. 임베딩 벡터를 통해 이 세 값들을 위와 같이 구한다. 여기서 'I love you'라는 문장을 통해 각 단어의 query, key, value를 구하기 때문에 'Self' Attention이라고 부르는 것 같다.

(여기서 $W_{Query}, W_{Key}, W_{Value}$는 파라미터 행렬로 이 행렬들을 학습시키는 것으로 이해했다.)

Self attention의 수식은 아래와 같다.

$${\rm Attention}(Q, K, V ) = {\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V$$

출처 : https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

위 이미지와 같이 한 단어에 대한 Attention값을 구한다. 이 것을 행렬연산으로 바꾸면 input 전체에 대한 Attention값을 한번에 구할 수 있다고 한다.

Attention 수식을 보면 query와 key를 곲한 후에 $\frac{1}{\sqrt{d_k}}$만큼 스케일링한 것을 볼 수 있다. Query와 key값을 곱한 값을 그냥 넣어주면 값이 커져 소프트맥스 함수의 기울기가 작은 곳으로가게 되는데 이것을 방지하기 위해서 스케일링했다고 한다.

 

3.2.2 Multi-head attention

지금까지 self-attention에 대해 설명을 했는데, 이 논문에서 쓴 것은 'Multi-head attention'이다. 그렇다면 multi-head attention은 무엇일까?

수식부터 살펴보면 아래와 같다.

$${\rm MultiHead}(Q, K, V ) = {\rm Concat}(head_1, \cdots, head_h)W^O$$

$${\rm where}\quad head_i = {\rm Attention}(QW^Q_i , KW^ K_ i , V W^V _i )$$

그림으로 표현하면 아래와 같이 나타낼 수 있다.

출처 : https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

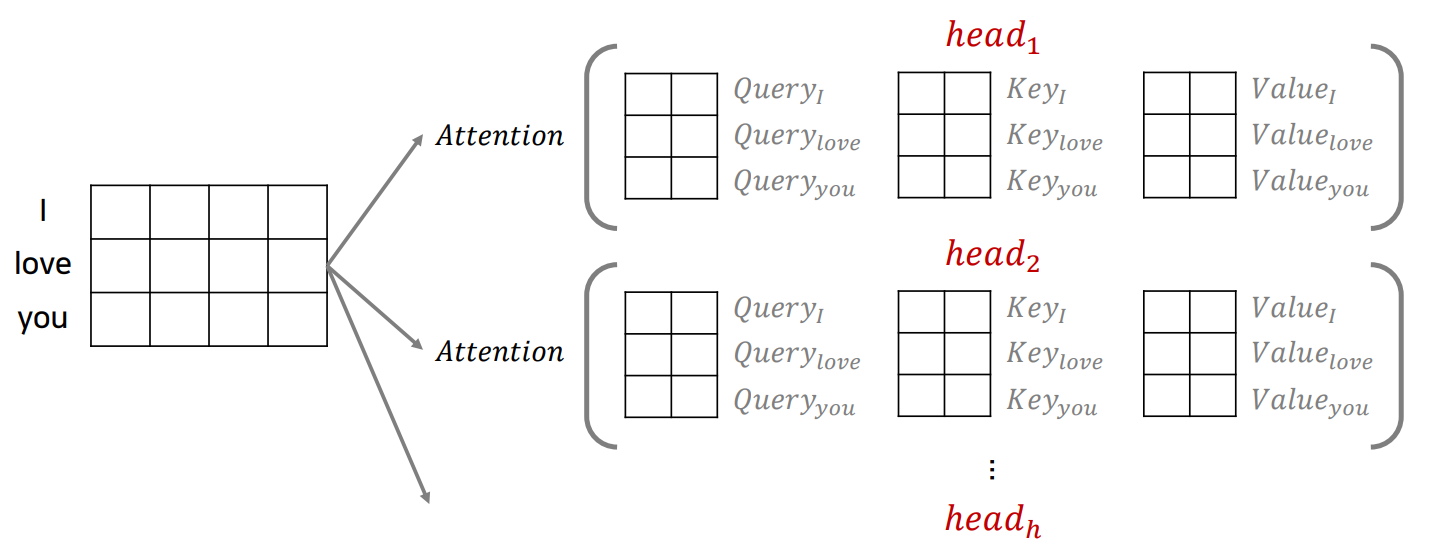
논문에서는 $h = 8$로 두어 $d_k = d_v = d_{model}/h = 64$로 query, key, value의 차원을 맞췄다고 한다. 이런식으로 해서 multi-head attention의 결과로 나온 output의 차원을 원래의 차원가 맞출 수 있었다고한다.​ 

 

3.2.3 Applications of Attention in our Model

이 논문에서 총 3종류의 Attention을 사용했다고 한다.

 

• Encoder-Docoder attention

쿼리는 이전 디코더 계층에서 오고 메모리 키와 값은 인코더의 출력에서 나온다. 이를 통해 디코더의 모든 위치가 입력 시퀀스의 모든 위치에 대해 attention을 기울일 수 있다. 이 Attention은 디코더의 두 번째 Multi-head attention에서 사용된다.

 

• Encoder Self Attention

인코더의 각 위치는 인코더의 이전 레이어에 있는 모든 위치에 attend할 수 있다.

 

• Masked Decoder Self Attention

디코더에서 쓰이는 Attention에서 '나는 그녀를 좋아한다.'라는 문장을 출력한다고 가정하면,  '그녀를'이라는 단어를 출력할 때 '좋아한다.'라는 단어를 알면 '그녀를'이라는 단어를 더 쉽게 출력할 수 있다. 그렇기 때문에 이러한 일종의 치팅을 방지하기 위해 뒷 부분의 Attention energy값에 $-\infty$​를 곱해 참고하지 않도록 하는 self attention을 적용한다. 

파란박스는 인코더, 초록박스는 디코드의 출력을 의미한다.

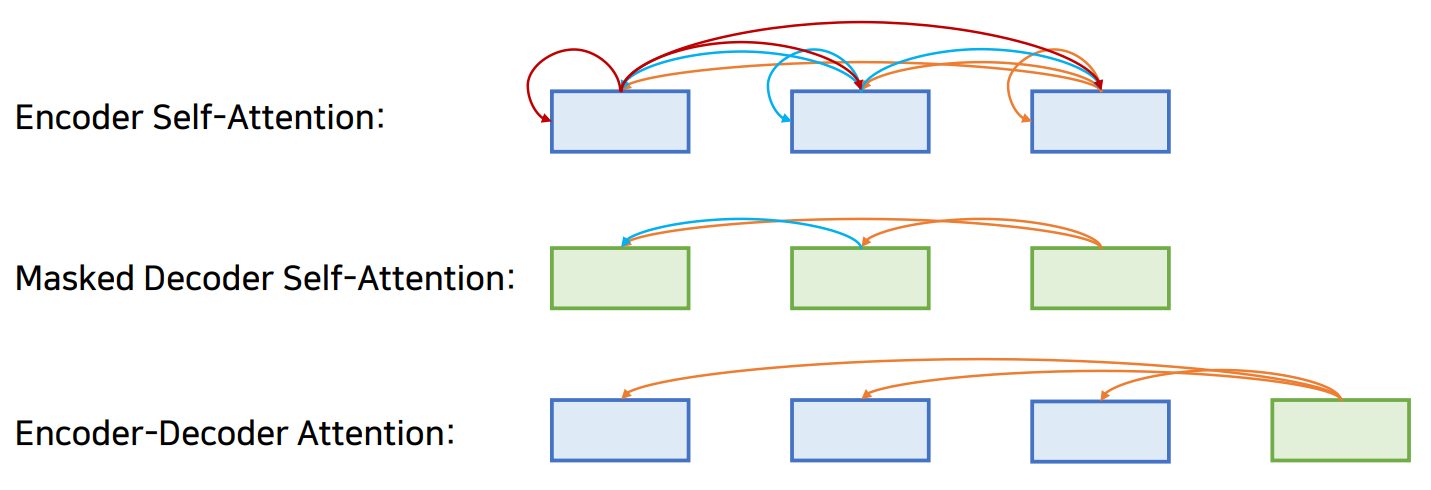
Layer가 4인 트랜스포머를 간단히 도식화하면 아래와 같이 나타낼 수 있다.

마지막 Encoder의 output은 모든 Decoder의 Input으로 들어간다.

3.3 Position-wise feed forward network

Encoder와 decoder 모두 attention 연산이 수행되고 나면 그 output은 fully connected feed forward network에 들어간다. 이 네트워크에서도 동일하게 residual learning 방식이 사용된다. 이 feed forward network를 수식으로 나타내면 아래와 같다.

$${\rm FFN}(x) = {\rm max}(0, xW_1 + b_1)W_2 + b_2$$

두 개의 선형변환과 그 사이에 ReLU activation으로 구성된다. 이 네트워크도 attention과 동일하게 모든 layer에서 같은 형태로 수행되고 layer마다 다른 파라미터를 가진다.

4. Why Self-Attention

이 논문에서 Self-Attention이 Recurrent와 Convolution보다 좋다는 것을 세가지의 조건??으로 보여준다.

1. the total computational complexity per layer

보통의 경우 $n$이 $d$보다 작기 때문에 레이어 당 계산 복잡도는 self-attention이 recurrent와 convolution을 사용할 때보다 작다고 한다.

 

2. the amount of computation that can be parallelized

Sequence 모델은 input이 들어오는 순서대로 계산이 되지만 Self-attention 모델은 input이 들어오면 input 전체를 한번에 계산이 되어진다. Sequential Operations가 $O(1)$이 된다. 그렇기 때문에 parallel system에 유리하다. 

 

3. the path length between long-range dependencies 

Long-range dependency를 학습하는 것은 많은 시퀀스 transduction 작업에서 핵심 과제다. 이러한 종속성을 학습하는 능력에 영향을 미치는 한 가지 핵심 요소는 네트워크에서 forward/backward signals가 통과해야 하는 경로의 길이다. 입력 및 출력 시퀀스의 모든 위치 조합 사이의 경로가 짧을수록 long-range dependency를 학습하기가 더 쉽다. 

Self-attention은 input을 한번에 처리해서 경로가 짧다고 이해했는데, 아닌 것 같다... 이 부분은 제대로 이해하지 못했지만 암튼 결과를 보면 maximum path length가 $O(1)$로 짧은 것을 확인 할 수 있다.

 

부수적인 이점으로 Self-attention은 더 해석 가능한 모델을 양상할 수 있다고 한다.

 

Training 세부사항과 실험 결과는 논문에 자세히 나오기 때문에 생략하도록 하겠다.

 

5. Conclusion

Attention 메커니즘만 사용해서 모델을 만들어 기존의 모델들보다 성능이 좋다는 것이 놀라웠다. 최근의 모델들을 보면 텍스트 데이터 뿐만 아니라 이미지 등에도 이용되는 것 같아서 꾸준히 transformer관련 모델들을 공부해야겠다는 생각이 들었다.

 

많이 부족해서 적극적인 피드백을 주시면 감사하겠습니다!