| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- flow matching
- diffusion models
- 네이버 부스트캠프 ai tech 6기
- image generation
- image editing
- memorization
- flow matching models
- VirtualTryON
- rectified flow
- 3d editing
- 3d generation
- transformer
- 프로그래머스
- 논문리뷰
- inversion
- Programmers
- shortcut model
- diffusion model
- diffusion
- Vit
- video generation
- visiontransformer
- 코딩테스트
- ddim inversion
- video editing
- DP
- Python
- BOJ
- freeinv
- 코테
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] Classifier-Free Diffusion Guidance 본문
[평범한 학부생이 하는 논문 리뷰] Classifier-Free Diffusion Guidance
junseok-rh 2024. 4. 13. 00:31https://arxiv.org/abs/2207.12598
Classifier-Free Diffusion Guidance
Classifier guidance is a recently introduced method to trade off mode coverage and sample fidelity in conditional diffusion models post training, in the same spirit as low temperature sampling or truncation in other types of generative models. Classifier g
arxiv.org
1. Introduction
Clasiifier Guidance는 학습된 classifier를 이용해 diffusion model의 sample 품질을 올리는 기법이다. (이에 대한 포스팅은 여기에서 볼 수 있다.) 본 논문에서는 classifier없이 classifier guidance가 수행되는 것에 흥미를 가지고 연구를 시작했다. Classifier guidance는 extra classifier를 훈련시켜야하기 때문에 diffusion model training pipeline을 복잡하게 만들고 noisy data로 학습되어야하기 때문에 pre-train된 classifier를 plug in 할 수 없다. 게다가 classifier guidance는 score estimate와 classifier gradient를 sampling 동안 mix하기 때문에, classifier-guided diffusion sampling이 image classifier가 gradient-based adversarial attack으로 혼동하도록 시도하는 것으로 해석될 수 있다. 이는 단순히 classifier에 대한 adversarial이기 때문에 FID와 IS같은 classifier-based metrics에 성공적으로 boost할 수 있었다는 의문이 제기될 수 있다. Classifier gradient의 방향으로 stepping하는 것은 특히 비모수적인 generators를 가진 GANs와 또한 닮았다. 이는 이미 classifier-based metrics에서 좋은 성능을 보인 GANs와 닮기 시작했기 때문에 그러한 metrics에서 좋은 성능을 보였다는 의문 또한 제기할 수 있다.
이러한 문제들을 해결하기 위해 본 논문은 classifier-free guidance를 제시한다. 이는 classifier를 피하는 방식이다. 이는 image classifier의 gradient 방향으로 sampling하기 보다는 conditional diffusion model의 score estimates와 joint하게 학습된 unconditional diffusion model의 score estimates를 섞는다. Mixing weight를 섞음으로써, classifier guidance에서 얻어진 것과 유사한 FID/IS trade off를 얻는다. Classifier-free guidance는 다른 generative model들이 가능한 높은 fidelity sample합성을 순수 generative diffusion models가 가능하다는 것을 보여줬다.
2. Background
본 논문에서는 continuous time에서 diffusion model을 학습시킨다. $x \sim p(x)$이고 $ z = \{z_\lambda | \lambda \in [\lambda_{min}, \lambda_{max}]\}$를 hyperparameter로 하면, forward process $q(z|x)$는 variance-preserving Markov process이다:
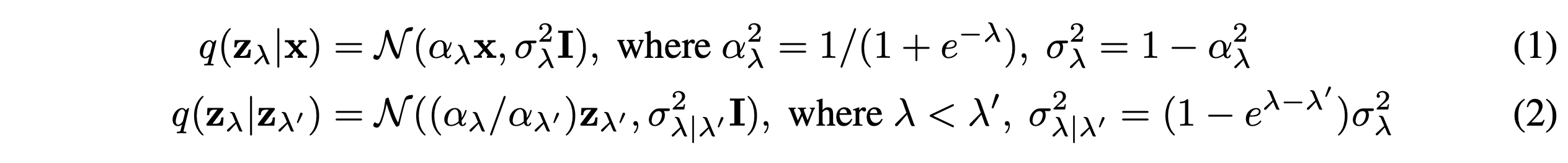
본 논문에서 $x \sim p(x)$이고 $z \sim q(z|x)$일 때, $z(z_\lambda)$의 marginal을 $p(z)(p(z_\lambda))$로 표기한다. $\lambda = {\rm log}\alpha^2_\lambda / \sigma^2_\lambda$이다. 그래서 $\lambda$는 $z_\lambda$의 log signal-to-noise ratio로 해석될 수 있다. 그리고 forward process는 $\lambda$가 줄어드는 방향으로 진행된다.
$x$에 대해 condition되면, forward process는 transition $q(z_{\lambda^\prime|z_\lambda},x) = \mathcal{N}(\tilde{\mu}_{\lambda^\prime|\lambda}(z_\lambda,x),\tilde{\alpha}^2_{\lambda^\prime|\lambda}I)$의 reverse로 표현될 수 있다. 이때 평균과 분산은 아래와 같다.
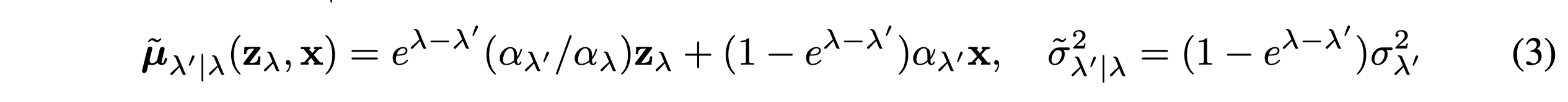
Reverse process는 $p_\theta(z_{\lambda_{{min}}}) = \mathcal{N}(0,I)$로 부터 시작한다. Transition은 아래와 같이 특정화한다.
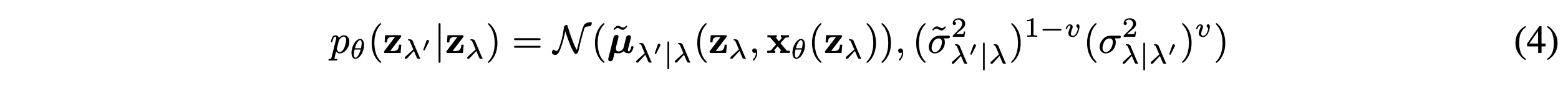
샘플링 동안, T time steps에 대해 $\lambda_{min} = \lambda_1 \leq \cdots \leq \lambda_T = \lambda_{max}$인 증가하는 수열에 따라 이 transition을 적용한다. 즉 discrete time ancestral sampler를 따른다. 만약 모델 $x_\theta$가 정확하면, $T \rightarrow \inf$에 따라 sample paths가 $p(z)$에 분포한 SDE로 부터 sample들을 얻는다. 그리고 continuous time model distribution을 나타내기 위해 $p_\theta(z)$를 사용한다. 분산은 Improved DDPM에서 제안된 것처럼 $\tilde{\sigma}^2_{\lambda^\prime|\lambda}$와 $\sigma^2_{\lambda^\prime|\lambda}$의 log-space interpolation이다. 본 논문에서 학습된 $z_\lambda$ dependent한 $v$보다는 상수 hyperparameter $v$를 사용하는 것이 더 효율적이라는 것을 발견했다.
Reverse process 평균은 $q(z_{\lambda^\prime}|z_\lambda,x)$에 연결된 추정치 $x_\theta(z_\lambda) \approx x$로 부터 온다. $\epsilon$-prediction의 관점에서 $x_\theta$를 다음과 같이 parameterize할 수 있다.
$$x_\theta(z_\lambda) = \frac{(z_\lambda-\sigma_\lambda\epsilon_\theta(z_\lambda))}{\alpha_\lambda}$$
그리고 아래와 같은 목적함수로 학습시킨다.
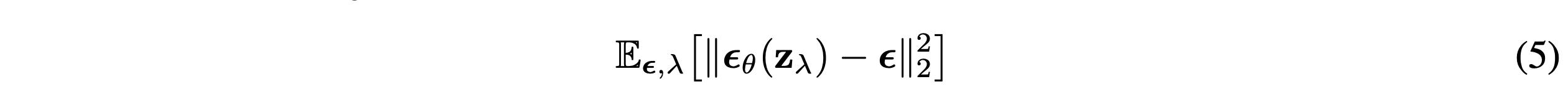
여기서 $\epsilon \sim \mathcal{N}(0,I), z_\lambda = \alpha_\lambda x + \sigma_\lambda\epsilon$,그리고 $\lambda$는 $[\lambda_{min}, \lambda_{max}]$에 대한 분포 $p(\lambda)$로부터 왔다. 이 objective는 다양한 noise scales에 대한 denoising score matchingd이다. 그리고 $p(\lambda)$가 uniform일 때, objective는 지정되지 않은 decoder $p_\theta(x|z)$와 $z_{\lambda_{min}}$에서 prior에 대한 term을 무시하고 latent variable model $\int p_\theta(x|z)p_\theta(z)dz$의 marginal log likelihood에 대한 variational lower bound에 비례한다.
$p(\lambda)$가 uniform이면, objective는 weighting이 샘플 퀄리티를 위해 tune될 수 있는 weighted variational lower bound로 해석될 수 있다. 본 논문에서는 discrete time cosine noise schedule에 의해 영감을 받은 $p(\lambda)$를 사용한다. $\lambda$는 균등하게 분포된 $u \in [0,1]$에 대해 $\lambda = -2{\rm logtan}(au + b)$에서 $\lambda$를 샘플링한다. 이 때, $b = {\rm arctan}(e ^ {-\lambda_{max}/2})$이고 $a = {\rm arctan}(e^{-\lambda_{min}/2})-b$이다. 이는 bounded interval에 대해 support되도록 수정된 hyperbolic secant 분포를 나타낸다. 유한한 timestep 생성에 대해, 본 논문에서는 균등하게 spaced된 $u \in [0,1]$에 상응하는 $\lambda$를 사용하고, 최종적으로 생성된 샘플은 $x_\theta(z_{\lambda_{max}})$이다.
$\epsilon_\theta(z_\lambda)$에 대한 loss가 모든 $\lambda$에 대한 denoising score matching이기 때문에, 모델에 의해 학습된 score $\epsilon_\theta(z_\lambda)$는 noisy data $z_\lambda$의 분포의 log-density의 gradient 즉, $\epsilon_\theta(z_\lambda) \approx -\sigma_\lambda\nabla_{z_\lambda}{\rm log}p(z_\lambda)$를 추정한다. 그러나 제한되지 않은 신경망을 $\epsilon_\theta$를 정의하기 위해 사용하기 때문에, gradient가 $\epsilon_\theta$인 scalar potential이 존재할 필요는 없다.(이 부분은 이해하지 못했다...) 학습된 diffusion model로부터 샘플링하는 것은 Langevin diffusion을 사용해 원래 데이터 $x$의 conditional distribution $p(x)$에 수렴하는 분포 $p(z_\lambda)$의 연속으로부터 샘플링하는 것과 닮았다.
Conditional generative modeling의 경우, 데이터 $x$는 conditioning information $c$와 jointly하게 온다. 모델에 대한 유일한 수정사항은 reverse process function approximator가 input으로 $c$를 받는다는 것이다.
3. Guidance
GANs과 flow-based models과 같은 특정 generative models의 흥미로운 특징은 sampling time때 generative model에 noise inputs의 variance나 범위를 줄임으로써 truncated나 low temperature sampling을 수행하는 능력이다. 각 sample의 퀄리티를 상승시키는 반면 다양성을 줄이는 의도된 효과이다.
불행하게도, truncation이나 low temperature sampling을 diffusion model에 직접 구현하는 시도는 비효율적이다. 예를 들어, model score를 scaling하거나 reverse process에서 Gaussian noise의 variance를 줄이는 것은 diffusion model이 blurry, low quality 샘플들을 생성하는 것을 야기한다.
3.1 Classifier Guidance
이 부분에 대한 상세한 설명은 classifier guidance 논문 리뷰 포스팅에서 볼 수 있다.
DIffusion models에서 truncation-like effect를 얻기 위해 classifier guidance가 도입됐다. 여기서 diffusion score $\epsilon_\theta(z_\lambda,c) \approx -\sigma_\lambda \nabla_{z_\lambda} {\rm log}p(z_\lambda | c)$이 다음과 같이 임의의 classifier model $p_\theta(c|z_\lambda)$의 log likelihood의 gradient를 포함되어 수정된다.
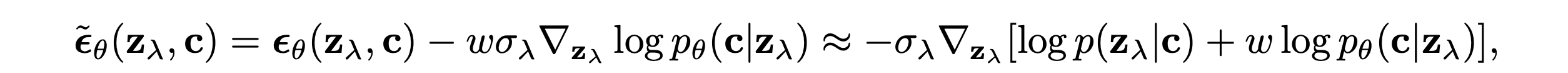
여기서 $w$는 classifier guidance의 강도를 컨트롤하는 파라미터이다. 수정된 score $\tilde{\epsilon}_\theta(z_\lambda,c)$는 diffusion model로 부터 샘플링할 때 $\epsilon_\theta(z_\lambda,c)$의 자리에서 사용된다. 그리고 이는 아래의 분포에서의 샘플들을 근사하는 것을 야기한다.

효과는 classifier $ p_\theta(c|z_\lambda)$가 정답 라벨에 높은 likelihood를 부여하는 데이터의 확률에 높은 가중치를 부여하는 것이다. 잘 분류되는 데이터는 perceptual quality의 Inception score에 높은 점수를 준다. 이는 설계상 생성모델에 보상을 준다. $w > 0$으로 셋팅함으로써 다양성을 줄이는 비용으로 diffusion model의 Inception score를 향상시킨다는 것을 발견했다.

위 이미지는 각 class에 대한 conditional distribution이 isotropic Gaussian인 세 개의 class의 예시에 대한 수치적으로 solved guidance $\tilde{p}_\theta(z_\lambda | c) \propto p_\theta(z_\lambda | c)p_\theta(c|z_\lambda)^w$의 효과를 보여준다. 위에서 guidance가 적용된 각 conditional의 형태는 뚜렷하게 non-Gaussian이다. Guidance의 힘이 커질수록, 각 conditional은 다른 class들로부터 probability mass를 멀리 그리고 logistic regression에 의해 주어진 높은 confidence의 방향으로 위치시킨다. 그리고 대부분의 mass는 더 작은 위치에 모여있게 된다. 이 현상은 ImageNet 모델에서 classifier guidance 강도가 증가할 때 발생하는 Inception score boost와 sample 다양성 감소의 간단한 징후로 보여질 수 있다.
Weight $w+1$인 classifier guidance를 unconditional model에 적용하는 것은 이론적으로 weight $w$인 classifier guidance를 conditional model에 적용하는 것과 동일한 결과를 낳는다. $p_\theta(z_\lambda | c)p_\theta(c|z_\lambda)^w \propto p_\theta(z_\lambda)p_\theta(c | z_\lambda)^{w+1}$이거나

이다. 그러나 흥미롭게도 class-conditional 모델에 classifier guidance를 적용할 때 가장 좋은 결과를 냈다고 한다. 이러한 이유로 본 논문에서는 conditional model에 guiding하는 setup을 적용한다.
3.2 Classifier-Free Guidance
본 논문에서는 image classifier로부터의 gradient에 의존하는 것과 섹션 1에서의 이유로 classifier를 제거하는 방식을 탐구한다. 본 논문에서는 이러한 gradient 없이 동일한 효과를 내는 classifier-free guidance를 소개한다. Classifier-free guidance는 classifier guidance와 동일한 효과를 가지는 $\epsilon_\theta(z_\lambda,c)$를 수정하는 대안적인 방식이다. 아래는 훈련과 샘플링 알고리즘을 나태낸다.


개별의 classifier model을 학습시키는 대신에, 본 논문은 score estimator $\epsilon_\theta(z_\lambda,c)$를 통해 parameterize된 conditional model $p_\theta(z|c)$와 함께 $\epsilon_\theta(z_\lambda)$로 parameterize된 unconditional denoising diffusion model $p_\theta(z)$을 학습하는 것을 선택했다. 본 논문에서는 두 model을 동시에 parameterize하기 위해 single neural network를 사용한다. Unconditional model을 위해 본 논문에서는 score를 예측할 때, class identifier $c$에 null token $\emptyset$를 넣는다. ($\epsilon_\theta(z_\lambda) = \epsilon_\theta(z_\lambda,c = \emptyset)$) 본 논문에서는 $c$를 하이퍼파라미터로 $p_{uncond}$라는 확률로 unconditional class identifier $\emptyset$으로 둠으로써 unconditional과 conditional 모델을 동시에 학습시킨다. 아래의 conditional과 unconditional score estimate의 linear combination을 따라서 샘플링을 수행한다.
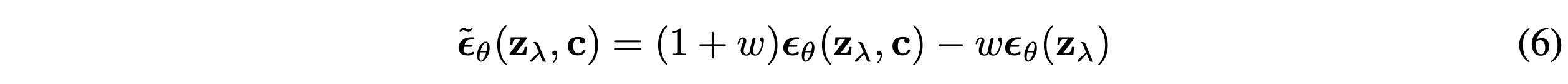

4. Experiments
본 논문에서의 실험의 목적은 classifier-free guidance가 classifier guidance와 유사하게 FID/IS tradeoff를 얻을 수 있다는 것을 보이는 것이다. 이를 위해 classifier gudance 논문과 동일한 아키텍처와 하이퍼파라미터를 사용한다. 개별의 classifier를 사용하지 않기 때문에 이전의 연구보다 더 적은 모델 용량을 사용한다. 그렇지만 경쟁적인 결과 혹은 이전의 연구보다 더 좋은 성능을 낸다.
4.1 Varying the Classifier-Free Guidance Strength
Classifier-free guidance가 classifier guidance나 GAN truncation과 유사한 방식으로 IS와 FID를 trade off할 수 있다는 것을 보인다. 아래의 결과는 64*64와 128*128 ImageNet 모델에 대한 guidance strength $w$를 바꾸면서 실험한 결과이다.


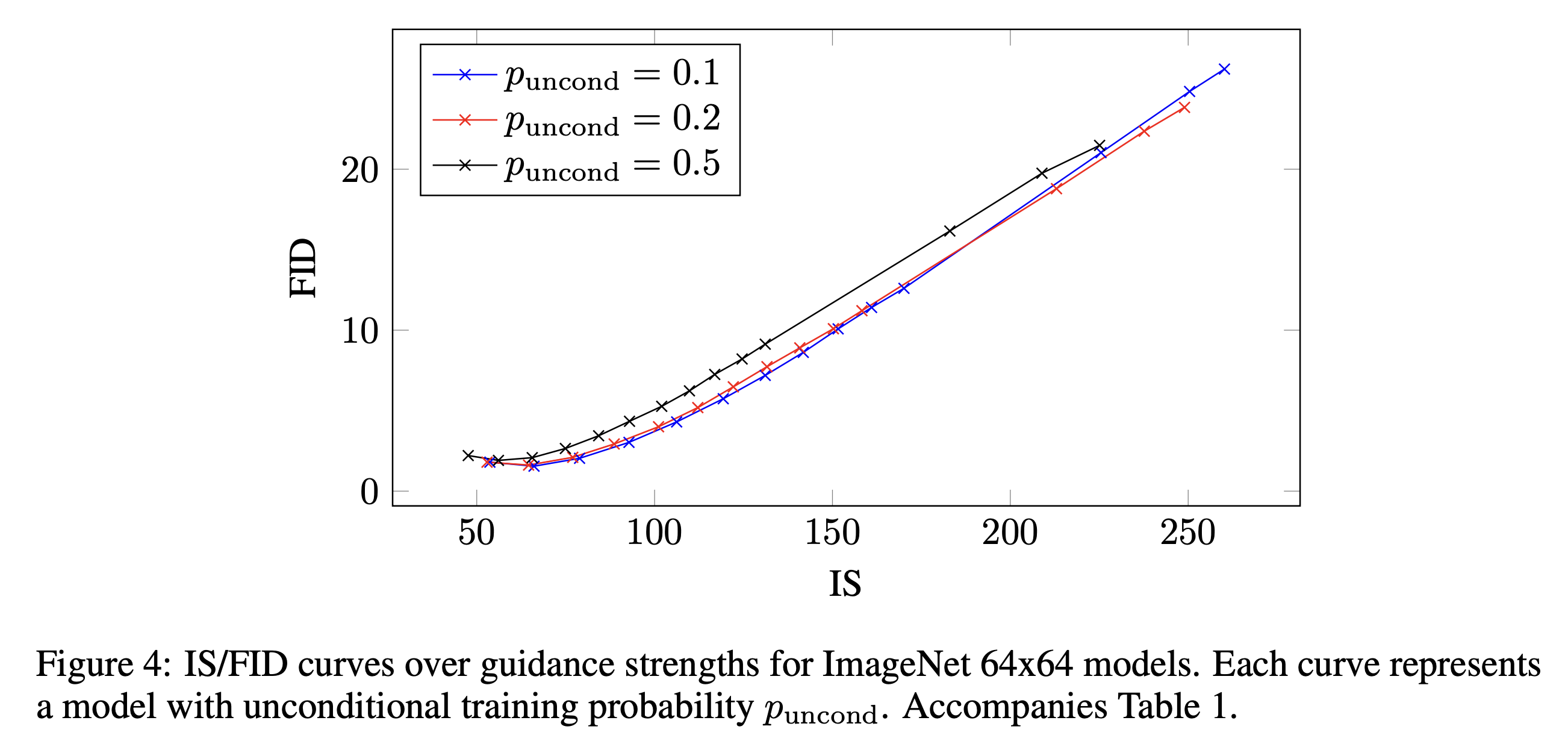
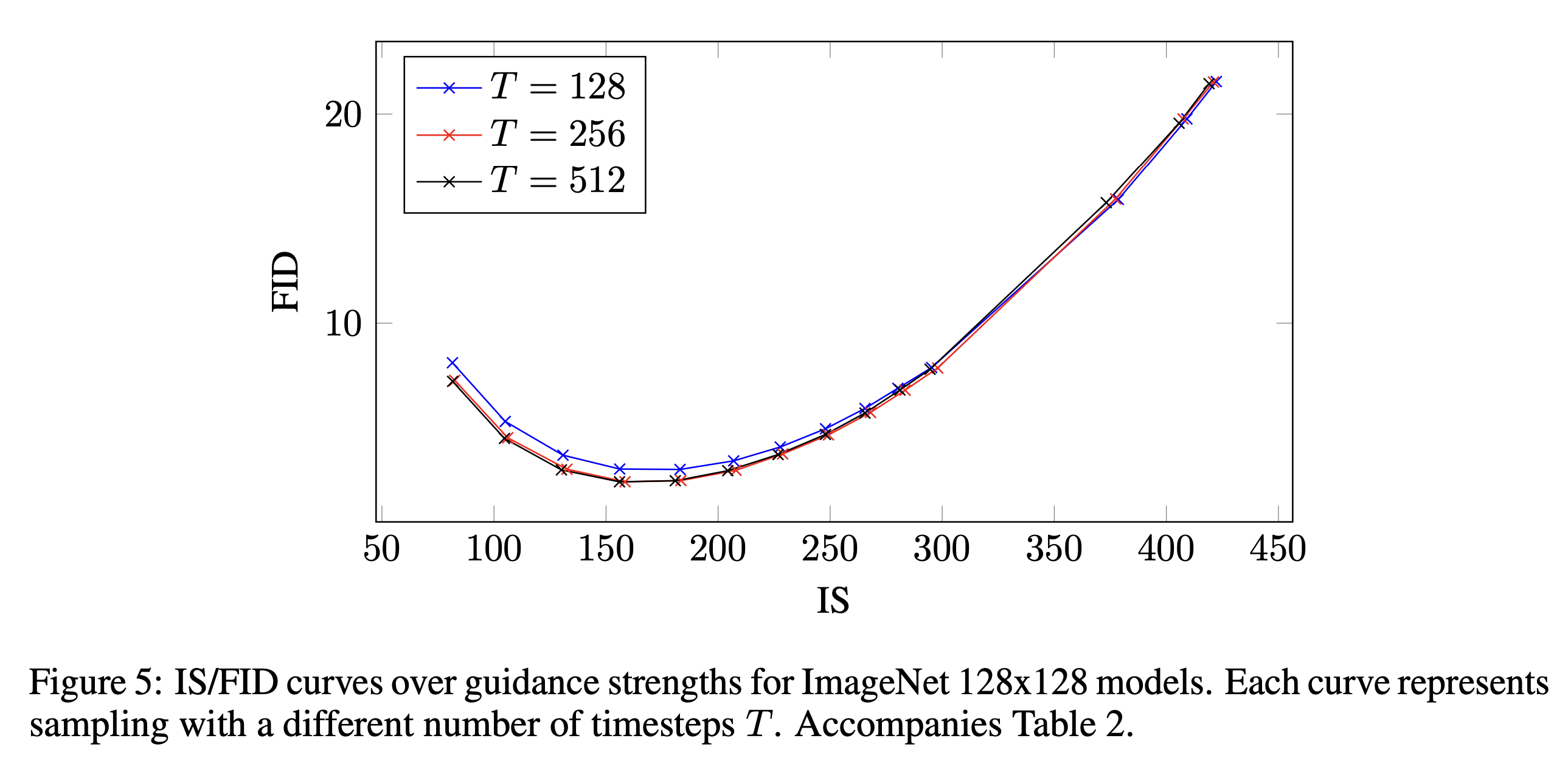
Guidance가 적을 때 최고의 FID를 얻었고, strong guidance에서 최고의 IS를 얻었다. 이를 통해 명백한 두 metrics에 대한 tradeoff를 얻었다.
아래의 이미지들은 다른 수준의 guidance를 통해 생성된 이미지들의 결과이다.


이를 통해 classifier-free guidance 강도를 증가하면 다양성은 줄지만 fidelity가 증가하는 것을 볼 수 있다.
4.2 Varying the Unconditional Training Probability
이번 섹션에서는 unconditional model을 학습시키는 확률에 대한 실험에 대한 결과를 설명한다. 4.1섹션에 표 1과 이미지 4에 $p_{uncond}$를 바꿔서 한 실험의 결과가 나와있다. $p_{uncond}$가 0.5일 때 공통적으로 결과가 안좋았다. 상대적으로 적은 부분의 모델 용량이 unconditional generation task에 바쳐질 필요가 있다는 결론이 나온다.
4.3 Varying th Number of Sampling Steps
이번 섹션에서는 sampling steps 수 T에 따른 결과를 설명한다. 4.1섹션에서 표 2와 이미지 5에 T를 바꿔서 한 실험의 결과가 나와있다.
256일 때, 샘플 퀄리티와 샘플링 속도에서 좋은 밸런스를 보였다.
5. Discussion
Classifier-free guidance의 가장 실용적인 이점은 extreme simplicity이다. Training시에는 랜덤하게 conditioning을 drop out하는, sampling시에는 conditioning과 unconditioning score estimate를 섞는 코드 한줄만 바꾸면 된다. 그리고 본 논문에서는 guidance가 pure generative모델로 수행 가능하다는 것을 보인다.
Classifier-free guidance의 잠재적 disadvantage는 바로 샘플링 속도이다. 또한 guidance는 샘플의 다양성을 낮추고 샘플의 퀄리티를 올리는 방식이라는 점이 있다.





