| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- VirtualTryON
- Programmers
- flow matching
- diffusion
- 네이버 부스트캠프 ai tech 6기
- video generation
- inversion
- Machine Unlearning
- 코테
- visiontransformer
- memorization
- diffusion models
- video editing
- Concept Erasure
- image generation
- ddim inversion
- 3d generation
- BOJ
- 프로그래머스
- rectified flow matching models
- unlearning
- image editing
- flow matching models
- rectified flow models
- rectified flow
- Python
- 3d editing
- 논문리뷰
- flow models
- diffusion model
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] A Latent Space of Stochastic Diffusion Models for Zero-Shot Image Editing and Guidance (ICCV 2023) 본문
[평범한 학부생이 하는 논문 리뷰] A Latent Space of Stochastic Diffusion Models for Zero-Shot Image Editing and Guidance (ICCV 2023)
junseok-rh 2024. 7. 18. 16:42깃헙 : https://github.com/ChenWu98/cycle-diffusion
GitHub - ChenWu98/cycle-diffusion: [ICCV 2023] A latent space for stochastic diffusion models
[ICCV 2023] A latent space for stochastic diffusion models - ChenWu98/cycle-diffusion
github.com
1. Introduction
기존에 deterministic한 DPM(Diffusion Probabilistic Models)의 denoising process는 invert될 수 있다. 하나의 deterministic한 noise $z$에서 하나의 이미지 $x$가 고정적으로 생성된다. 그리고 이러한 DDIM inversion?은 이미지 editing에서 많이 사용됐다고 한다.
본 논문에서는 이러한 속성을 stochastic한 DPM으로 확장해서 모든 timestep $t$에서의 추가되는 gaussian noise들을 모두 concat해서 latent를 만들고 이러한 latent가 이미지 $x$에 대한 latent code가 되는 방식을 제안한다. 본 논문에서 제안한 latent code로 기존 idea를 deterministic한 DPM에서 stochastic한 DPM으로 확장시킨다.

2. Method
2.1 Gaussian Latent Space for Diffusion Models
Deterministic DPM에서는 latent $z$가 주어지면 정해진 이미지 $x$가 생성된다. 결국 deterministic DPM은 latent code $z$에서 이미지 $x$ 로의 deterministic한 mapping $G : \mathbb{R} \rightarrow \mathcal{X}$으로 볼 수 있다.

본 논문에서는 stochastic DPM도 latent $z$에서 이미지 $x$로의 deterministic mapping으로 표현될 수 있다는 것을 보인다.

위의 수식 1을 통해 latent $z$와 mapping $G$를 다음과 같이 나타낼 수 있다.


2.2 DPM-Encoder
Stochastic DPM을 사용해서 이미지 $x$로부터 latent code $z$를 샘플링하기 위해, 본 논문에서는 DPM-Encoder를 제안한다. 각 이미지 $x := x_0$에 대해, stochastic DPM은 posterior distribution $q(x_{1:T}|x_0)$를 정의하고 이와 수식 4를 통해 다음과 같이 $z \sim DPMEnc(z|x,G)$를 이끌어낼 수 있다.


DPM-Encoder의 특성은 완벽한 reconstruction이다. 이는 모든 $z\sim Enc(z|x,G)$에 대해 $x = G(z)$를 가진다는 것을 의미한다.
2.3 Application 1 : Edit Images with CycleDiffusion
본 논문에서는 CycleDiffusion이라는 image-to-image translation 방식을 제안한다. Source image $x \in \mathcal{D}_1$가 주어지면, DPM-Encoder를 통해 $z$로 인코딩하고 $G_2$로 디코딩해서 $\hat{x} = G_2(z)$를 얻는다.
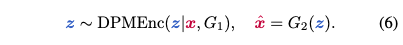
또한 두 개의 text로 condition된 image 분포 $\mathcal{D}_1, \mathcal{D}_2$를 정의함으로써 text-to-image diffusion model로 CycleDiffusion모델을 적용할 수 있다. 또한 다음과 같이 zero-shot image-to-image editing도 수행할 수 있다.
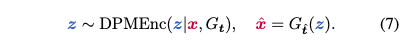
여기서 $G_t$는 text $t$에 대해 condition된 text-to-image diffusion model이고, $t$는 이미지 $x$에 대한 설명이다. CycleDiffusion의 알고리즘은 다음과 같다.

An analysis for image similarity with fixed $z$
Text-to-image 모델이 다음 두 가지 속성을 가진다고 가정하자.
- 동일한 text에 condition되면, 유사한 noisy image는 유사한 prediction을 이끈다. $\Vert \mu_T(x_t,t|t) - \mu_T(\hat{x}_t,t|T) \Vert \leq K_t \Vert x_t - \hat{x}_t \Vert$, $\mu_T(x_t,t|t)$는 $K_t$-Lipschitz이다.
- 동일한 이미지가 주어질 때, 두 texts는 유사한 prediction을 이끈다. $\Vert \mu_T(\hat{x}_t,t|t) - \mu_T(\hat{x}_t,t|\hat{t}) \Vert \leq S_t$. 직관적으로 $t$와 $\hat{t}$사이의 차이가 작을수록 작은 $S_t$를 준다.
동일한 latent code $z$가 샘플링에서 사용될 때 timestep $t$에서 $\Vert x_t - \hat{x}_t \Vert$의 상한을 $B_t$라 하자. $B_T = 0$이고 $B_0$는 생성된 이미지들의 $\Vert x - \hat{x} \Vert $의 상한이다. 상한 $B_t$는 시간에 따라 전파된다. 위 두 개의 특성을 결합하면 다음을 얻을 수 있다.

이렇게 text-to-image diffusion model을 통해 이미지의 유사성을 분석한다.
2.4 Application 2 : Plug-and-Play Guidance
예를 들어서 $z \sim \mathcal{N}(0,I)$에서 시작해서 다음과 같은 Langevin dynamics를 통해 $z := z^{<n>}$를 샘플링할 수 있다.

위와 같은 방법을 통해 $z \sim p(z|\mathcal{C})$를 샘플링 할 수 있고 $x \sim p(x|\mathcal{C})$를 샘플링하는 것은 $z \sim p_z(z|\mathcal{C}), x = G(z)$에서 샘플링하는 것과 동일하기 때문에 $\mathcal{C}$로 condition된 $x$를 샘플링할 수 있다.
3. Experiments
3.1 Unpaired Image-to-Image Translation
Metrics
FID, KID, PSNR, SSIM
Baselines
CIT, ILVR, SDEdit, EGSDE
Results
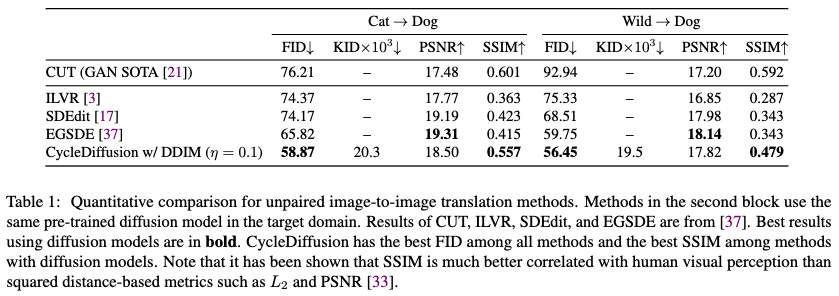

3.2 Zero-Shot Image Editing
Metrics
PSNR, SSIM, CLIP score, directional CLIP score
Baseline
SDEdit, DDIB
Results
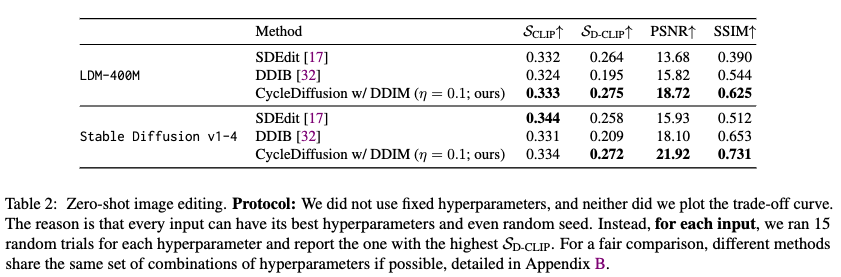


Compatibility with Cross Attention Control

최근 editing task를 다루다보니 editing 관련 논문을 읽는데 DDPM inversion을 이용한 기법들이 자주 나오길래 이와 관련된 논문을 쭉 읽어야 겠다는 생각이 들었다. 완전 최신 3D editing 논문들에서 슬슬 이러한 기법들을 적용하는 논문들이 나오고 있는데 이 쪽 논문들을 얼렁 읽고 내 연구에도 적용해봐야겠다




