| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- inversion
- masactrl
- 코딩테스트
- 코테
- diffusion models
- 3d generation
- transformer
- Programmers
- diffusion model
- video generation
- diffusion
- rectified flow
- 논문리뷰
- memorization
- 네이버 부스트캠프 ai tech 6기
- flipd
- flow matching
- segmentation map
- noise optimization
- visiontransformer
- video editing
- Python
- DP
- Vit
- VirtualTryON
- 프로그래머스
- segmenation map generation
- 3d editing
- BOJ
- image editing
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] An Editing Friendly DDPM Noise Space : Inversion and Manipulations (CVPR 2024) 본문
[평범한 학부생이 하는 논문 리뷰] An Editing Friendly DDPM Noise Space : Inversion and Manipulations (CVPR 2024)
junseok-rh 2024. 9. 18. 18:59GitHub - inbarhub/DDPM_inversion: Official pytorch implementation of the paper: "An Edit Friendly DDPM Noise Space: Inversion an
Official pytorch implementation of the paper: "An Edit Friendly DDPM Noise Space: Inversion and Manipulations". CVPR 2024. - GitHub - inbarhub/DDPM_inversion: Official pytorch implementa...
github.com
해결하려는 문제
본 논문에서는 기존 DDIM latent가 아닌 DDPM latent를 이용해 edit-friendly한 noise map을 제안해서 image editing하는 방법론을 제안한다.
1. Introduction
Diffusion model을 이용해서 여러 방식의 image editing 방식들이 있었는데, 이러한 방식들의 key challenge는 real content의 editing에 이용하는 것이다. 이를 위해서는 generation process를 역으로 진행해 주어진 이미지를 reconstruction하는 noise vector를 추출하는 과정을 필요로 한다. 하지만 이 부분이 major challenge이다.
DDIM inversion을 주로 사용해 왔는데, 이는 diffusion timestep의 수가 클 때 정확하고, text-guided editing에서는 sub-optimal이 종종 발생한다. 본 논문에서는 DDPM inversion을 다루는데, DDIM과 다르게 DDPM은 $T+1$개의 noise map이 generation process에 포함되고 이들은 각각 생성된 output과 같은 dimension을 지닌다. 그러므로 noise space의 전체 dimension은 output보다 크고 image를 perfect reconstruction하는 noise sequence가 무한히 많이 존재한다. 이 특성은 inversion process에서 유연성을 제공하는 반면, 모든 consistent inversion이 edit friendly하지 않다.
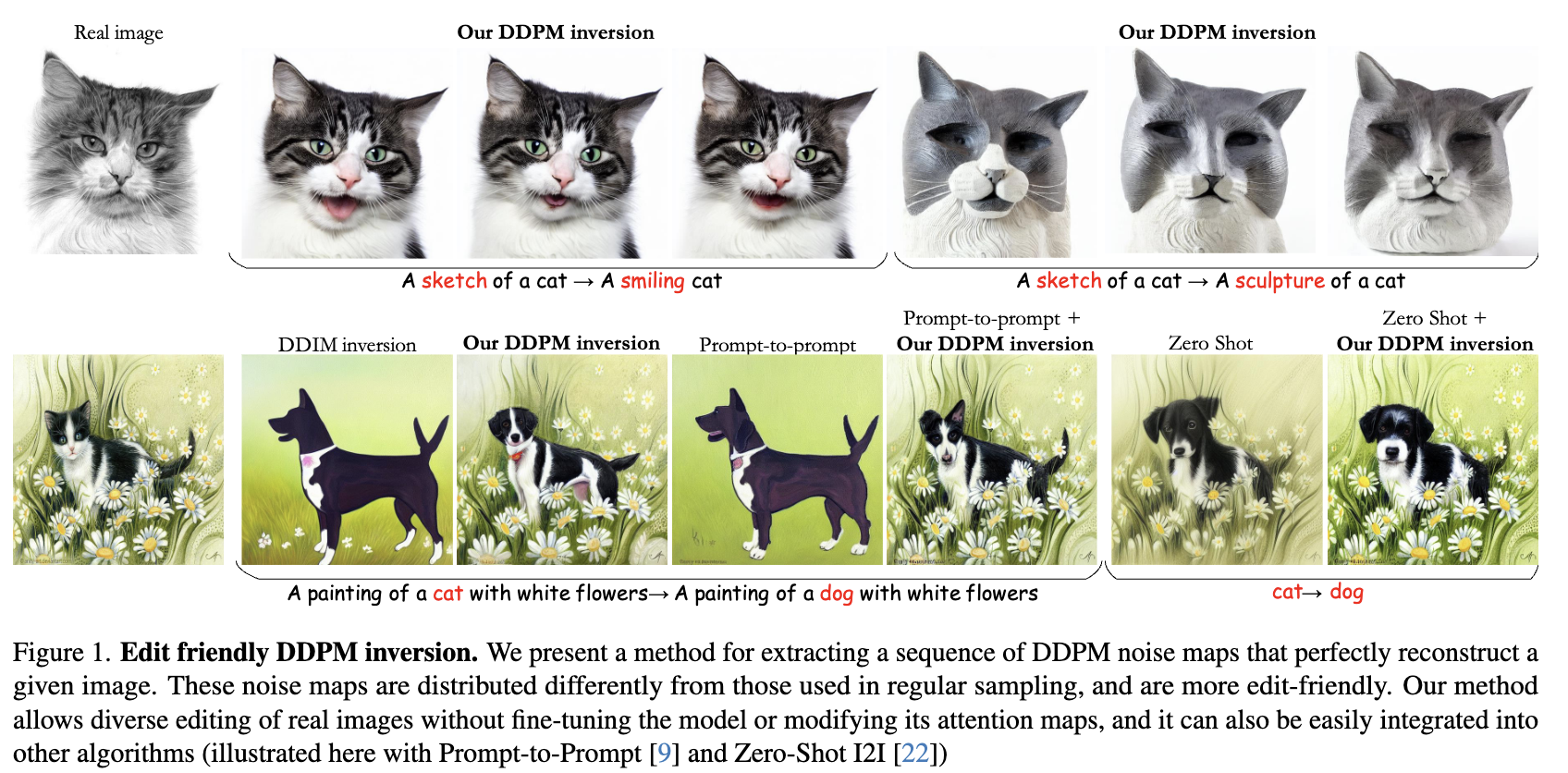
본 논문에서는 text guidance maipulation을 이용한 editing에 더 적합한 대안적인 inversion 방법론을 제안한다. 이 방식은 noise maps에 image를 더 강하게 찍어낸다. 그렇기에 구조를 더 잘 보존한다. 이는 본 논문의 noise map이 더 높은 분산을 가지기 때문에 그렇다고 한다. 본 논문의 방식은 optimization을 필요로 하지 않고 빠르고, 상대적으로 작은 diffusion step 수를 통해 sota의 결과를 냈다고 한다. 특히, 본 논문의 DDPM inversion은 기존의 DDIM inversion을 사용한 editing 방식에 쉽게 통합될 수 있다고 한다. 아래의 그림처럼 이는 original image에 대한 fidelity를 보존하는 능력을 향상시킨다고 한다. 또한 noise vector를 stochastic한 방식으로 찾기 때문에 text prompt에 모두 적합한 다양한 editing된 이미지 셋들을 제공할 수 있다.
2. The DDPM noise space
DDPM의 forward process는 다음과 같다.

이를 다음과 같이 표현할 수 있다.

위 식에서 $\{ \epsilon_t \}$이 independent하지 않다는 것이 주요하다. 각 $\epsilon_t$는 noise $n_0, \cdots, n_t$가 축적된 것에 대응되기 때문이다. 그래서 $\epsilon_t$와 $\epsilon_{t-1}$는 $t$에 correlate됐다.
Generative process는 random noise vector $x_T \sim \mathcal{N}(0,\mathbf{I})$에서 시작하고 다음을 이용해서 반복적으로 denoising한다.

여기서 $\{ z_t \}$는 iid standard normal vector이고,

이다. 여기서 $f_t$는 $x_t$에서 $\epsilon_t$를 예측하도록 학습된 neural network, $P(f_t(x_t)) = (x_t - \sqrt{1-\bar{\alpha}_t}f_t(x_t))/\sqrt{\bar{\alpha}_t}$는 예측된 $x_t$, $D(f_t(x_t)) = \sqrt{1-\bar{\alpha}_t-\sigma_t^2}f_t(x_t)$는 $x_t$의 direction pointing이다. Variance schedule은 $\sigma_t = \eta\beta_t(1-\bar{\alpha}_{t-1})/(1-\bar{\alpha}_t), \ \eta \in [0,1]$이다.
$\{ x_T,z_T, \cdots, z_t \}$는 (3)을 통해 생성된 유일한 image $x_0$를 결정한다. 본 논문에서는 다음 이미지처럼 이들을 latent code로 여긴다. 본 논문에서는 $x_0$를 생성하는 noise vector를 추출하는데에 관심을 가진다.
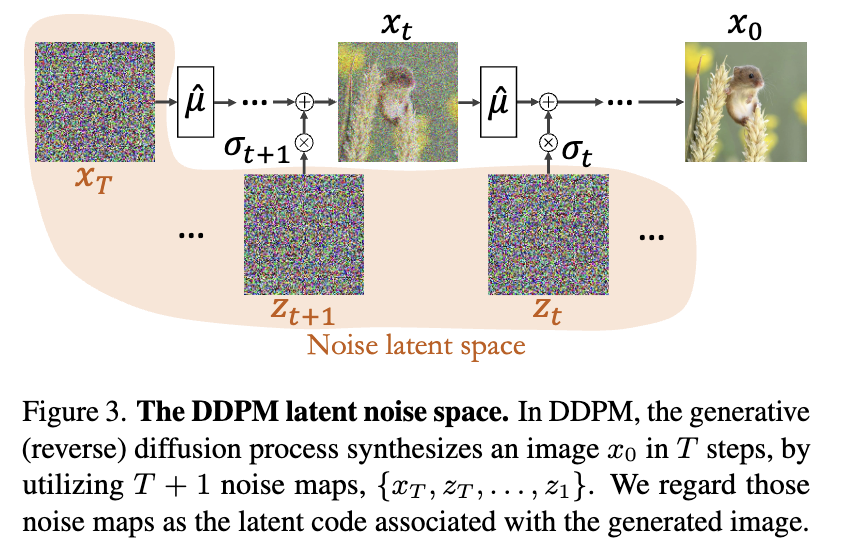
2.1 Edit friendly inversion
(3)번 식으로부터 다음과 같이 임의의 $T+1$개의 이미지 $x_0, \cdots, x_T$를 이용해서 일관성있는 noise map을 추출할 수 있다.
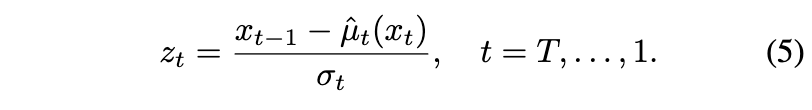
하지만 이렇게 임의의 sequence of image들이 조심스럽게 구성되지 않으면, $f_t(\cdot)$이 학습된 input의 분포와 거리가 멀어지게 된다. 이 경우에서 추출된 noise map들을 사용해서 text condition을 바꾸면 안 좋은 결과가 나타난다.
Naive한 접근 방식으로는 $x_T \sim \mathcal{N}(0, \mathbf{I})$에서 샘플링하는 것에서 시작해서 각 timestep $t = T, \cdots, 1$에 대해 (2)번식에서 $x_t$와 real image $x_0$를 이용해서 $\epsilon_t$를 추출한다. 이를 이용해서 (4)를 가지고 $\hat{\mu}_t(x_t)$를 계산하고 (3)를 통해 $x_{t-1}$를 구한다.
이 방식을 통해 얻은 noise maps은 generative process의 분포와 유사하게 분포한다. 하지만 이들은 global structure를 editing하는데에는 적합하지 않다. 아래 이미지에서 결과를 확인할 수 있는데, 이러한 결과가 나타나는 이유는 DDPM의 native noise space는 애초에 edit friendly하지 않는 것이다. 즉 우리가 ground-truth noise map을 가지고 있더라도, 이들을 고정하고 text prompt를 변경해도 이미지의 structure를 보존하지 않는다.

본 논문에서는 다음 수식을 통해 $x_0$로부터 $x_1, \cdots, x_T$를 구성하는 것을 제안한다.
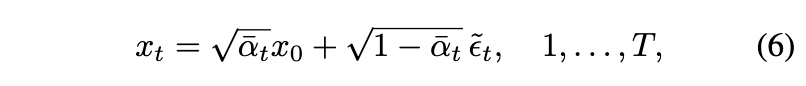
여기서 $\tilde{\epsilon}_t \sim \mathcal{N}(0, \mathbf{I})$는 통계적으로 독립이다. (6)과 (2)는 형태가 비슷하지만 근본적으로 다른 확률적인 process를 나타낸다. (2)에서는 연속적인 $\epsilon_t$의 모든 페어들은 highly correlate되어 있지만, (6)에서 $\tilde{\epsilon}_t$는 독립이다. 그래서 본 논문 구성에서는 $x_t$와 $x_{t-1}$는 (2)에서보다 멀리 떨어져있어서, (5)로부터 추출된 모든 $z_t$는 기존 generative process보다 더 높은 분산을 지닌다. 본 논문의 방식의 슈도코드는 다음과 같다.

이 방식에 대한 몇가지 의견이 있다.
- 이 방식은 input image를 machine precision까지 reconstruction한다.
- 적절한 형태의 $\hat{\mu}_t(\cdot)$를 사용함으로써 어떤 종류의 diffusion process에 대해서도 사용하기 간단하다.
- (6)에서의 랜덤성으로, 다양한 inversion을 얻을 수 있다. $\rightarrow$ 다양한 editing결과를 가져올 수 있고 이는 DDIM inversion은 못 가지는 특성이라고 함.
2.2 Properties of the edit-friendly noise space
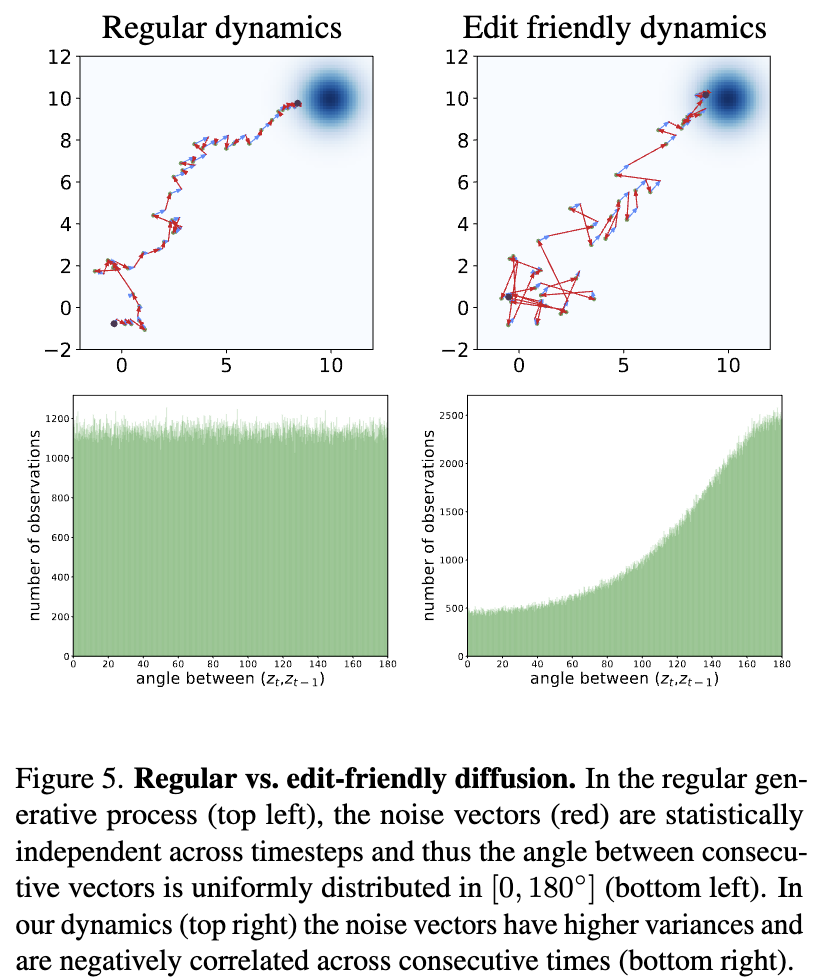
위 이미지는 diffusion model을 이용해서 $\mathcal{N} \left( \begin{pmatrix} 10 \\ 10 \end{pmatrix}, \mathbf{I} \right)$에서 sampling한 실험의 결과를 나타낸 것이다. 이는 $x_T \sim \mathcal{N} \left( \begin{pmatrix} 0 \\ 0 \end{pmatrix}, \mathbf{I} \right)$에서 시작한다. 그리고 $x_0$에서 끝나는 $\{ x_t \}$ sequence를 생성한다. 각 스텝은 deterministic $\hat{\mu}_t(x_t)$(파란 화살표)와 noise vector $z_t$(빨간 화살표)로 나뉜다. 왼쪽은 기존 ddpm inversion이고 오른쪽은 본 논문의 방식의 결과이다. 본 논문의 경우에서 $\{ z_t \}$가 더 크다. 이 특성은 $x_t$의 구성에서 오는데, (2)에서와 보다 $x_t$마다 멀리 떨어져있기 때문이라고 한다. 빨간 화살표가 더 길면서 어떻게 목적지로 가는 trajectory를 형성할 수 있을까하는 의문에 대해서 본 논문은 이는 연속적인 noise vector 사이의 각이 둔각을 띄는 경향 때문이라고 말하고 있다. 즉, 본 논문의 noise vector들이 연속적인 시간에 따라 negatively correlated되어있기 때문이라는 것이다.
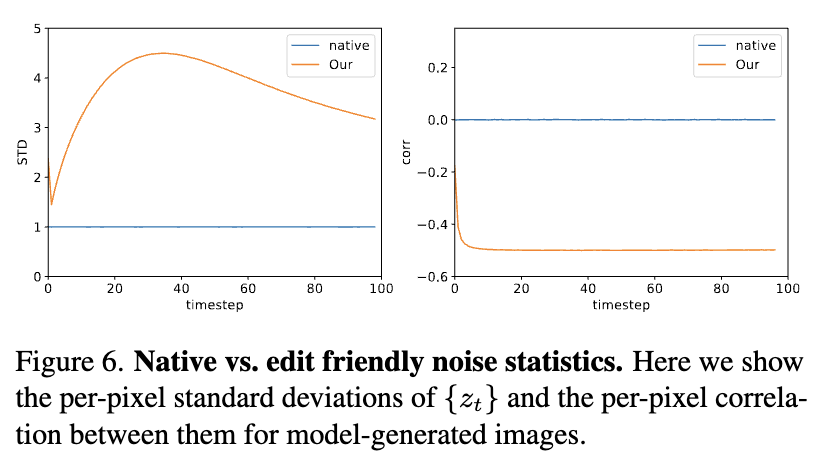
위에 나타난 특성들은 image generation에서도 동일하게 발생한다. 위 이미지는 $z_t$의 per pixel variance와 $z_t$와 $z_{t-1}$사이의 correlation을 나타낸다. 본 논문의 noise는 더 높은 variance와 연속적인 step사이에 대해서는 negative correlation을 나타낸다. 이러한 더 큰 variance noise vector는 input image의 구조를 더 강하게 encode하고 editing에 더 적합하다.
Image shifting

Image shifting은 단순히 latent noise들을 모두 shifting하는 것으로 가능하다. 위의 결과를 보면 native latent code를 shifting하는 것은 image structure의 완전한 loss를 야기한다. 반면에 본 논문의 edit-friendly code를 shifting하는 것은 최소한의 degradation을 보여준다.
Color manipulation
Input image $x_0$, binary mask $B$, 그에 상응하는 colored mask $M$가 주어졌다고 가정하자. $\{ x_1, \cdots, x_T \}$를 구성하고 (6)과 (5)를 통해 $\{ z_1, \cdots, z_T \}$를 추출하는 것으로 시작해서 다음과 같이 noise map을 수정한다.
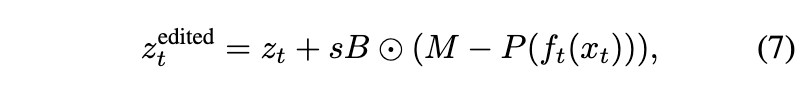
(4)로부터 $P(f_t(x_t))$를 가져오고, $s$는 editing strength를 controlling하는 파라미터이다. 이 modification은 $[T_1, T_2]$에 대해서 수행된다. 수식에서 괄호 안의 term은 desired color와 예측된 clean image 사이의 차이를 각 timestep마다 encode한다.

위 이미지는 SDEdit과 비교한 결과를 나타낸다. 본 논문의 방식은 texture를 수정하는 것 없이 강한 editing 능력을 보인다.
3. Text-Guided Image Editing
Real image $x_0$, text prompt $p_{src}$, target text prompt $p_{tgt}$가 주어졌다고 가정하자. 이 prompt에 대해서 이미지를 수정하기 위해서는, denoiser에 $p_{src}$를 주입하면서 edit-friendly noise maps $\{ x_T, z_T, \cdots, z_1 \}$를 추출한다. 그리고 나서 이를 고정하고 denoiser에 $p_{tgt}$를 주입하면서 이미지를 생성한다. 이 generation process는 $T- T_{skip}$에서 시작한다.


위 결과를 보면, 본 논문의 방식은 image의 구조를 유지하면서 semantic들을 수정하는 것을 볼 수 있다. 또 DDIM inversion에 의존하는 방식들에 본 논문의 inversion을 결합한 결과는 오른쪽 이미지에서 확인할 수 있다.
4. Experiments
Implementation details
- Stable diffusion을 사용했고, image size는 512*512*3, latent space는 64*64*4이다.
- Input image에 대한 faithfulness와 target prompt에 대한 adherence사이의 balance를 컨트롤하는 파라미터 classifier-free guidance와 $T_{skip}$가 있다.
- strength = 15, $T_{skip}$ = 36, $\eta$ = 1, 100 inference step을 사용했다.
Datasets
- modified ImageNet-R-TI2I, modified Zero-Shot I2IT
Metrics
- LPIPS : structure preservation의 정도
- CLIP score : 생성된 이미지가 text prompt를 따르는 정도
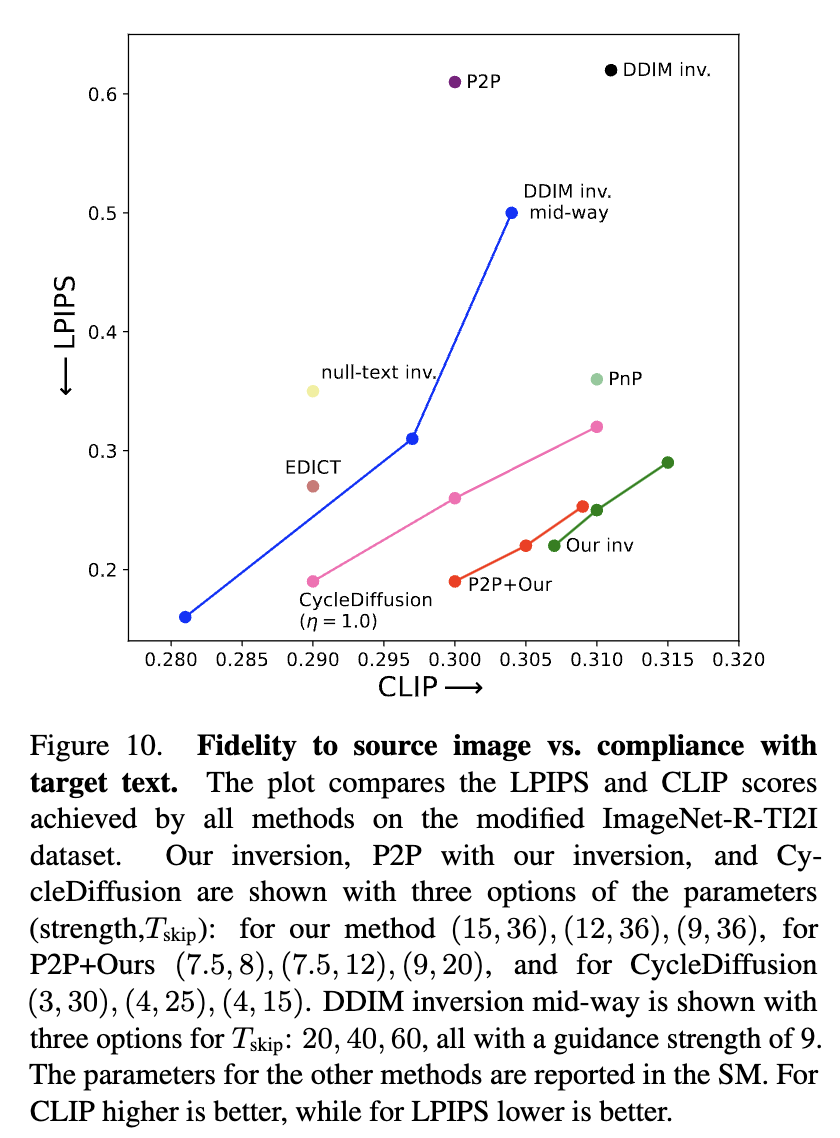
Comparisons on the modified ImageNet-R-TI2I dataset

Comparisons on the modified Zero-Shot I2IT dataset

5. Conclusion
본 논문에서 제시한 noise map은 기존의 noise map보다 더 강하게 image structure를 encode한다.





