| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 프로그래머스
- score distillation
- visiontransformer
- diffusion models
- Vit
- video editing
- 코테
- controllable video generation
- diffusion model
- style align
- emerdiff
- 3d editing
- VirtualTryON
- 3d generation
- segmenation map generation
- dreammotion
- video generation
- controlnext
- 논문리뷰
- segmentation map
- 코딩테스트
- magdiff
- DP
- transformer
- Python
- Programmers
- BOJ
- 네이버 부스트캠프 ai tech 6기
- image editing
- diffusion
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] Swin Transformer : Hierarchical Vision Transformer using Shifted Windows 본문
[평범한 학부생이 하는 논문 리뷰] Swin Transformer : Hierarchical Vision Transformer using Shifted Windows
junseok-rh 2023. 9. 19. 02:43직전에 ViT 논문을 리뷰했는데, 이번에는 ViT의 문제점을 개선하고 더 general한 task에서 사용가능 하도록 한 모델인 Swin Transformer 논문을 리뷰하려고 한다.
https://arxiv.org/abs/2103.14030
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
This paper presents a new vision Transformer, called Swin Transformer, that capably serves as a general-purpose backbone for computer vision. Challenges in adapting Transformer from language to vision arise from differences between the two domains, such as
arxiv.org
0. 기존 ViT의 단점
일단 기존 ViT는 패치 크기가 동일하게 적용되기 때문에 고밀도의 비전 작업에 적용하는데 한계가 있고, 계산량도 많다는 단점을 가진다.
이러한 단점들을 보완하기 위해 본 논문에서 소개하는 것이 Swin Transformer이다.
1. Abstract & Introduction
본 논문의 제목은 'Swin Transformer : Hierarchical Vision Transformer using Shifted Windows'이다. 제목에서 이 논문의 주요한 키워드를 고르면 Abstract와 Introduction에서 강조한 Hierarchical과 Shifted Windows 라고 할 수 있다.
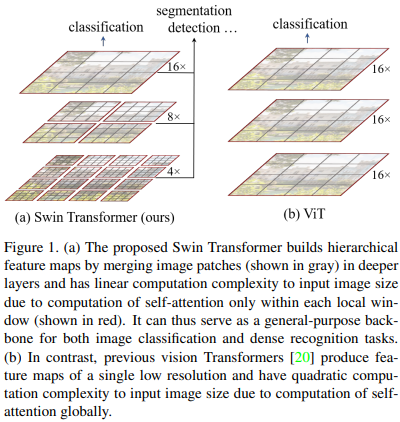
왼쪽 이미지에서 ViT를 보면 patch의 크기가 동일한 것을 볼 수 있다. 이 때문에 고밀도의 Vision Task에서 활용하기엔 제한이 된다. 고해상도의 이미지를 ViT에 넣게 되면 이미지 크기에 quadratic하게 계산량이 많아진다고 한다. 반면에 Swin Transformer를 보면 layer마다 patch의 크기가 달라지는 hierarchical한 representation을 구축한다. 이 덕분에 이미지 크기에 선형적으로 계산량이 많아져 기존 ViT보다 고해상도 이미지를 처리하는데 적합하다고 한다.
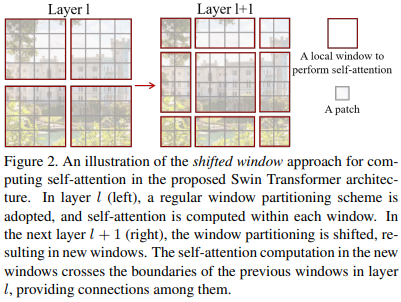
오른쪽 이미지를 보면 이미지를 window로 나누면 나누어지는 부분에서의 이미지 픽셀들의 self-attention이 계산되지 않는다. 하지만 shifted window 방식을 이용하면 나누어지는 부분의 픽셀들끼리도 self-attention을 계산할 수 있게 된다고 한다.
이제 Swin Transformer에 대해 자세히 알아보자.
2. Method
2.1 전체적인 아키텍처
$H \times W \times 3$인 이미지가 input으로 들어오면 Patch Partition과정을 통해(논문에서 patch의 크기를 $4 \times 4$로 함) 겹치지 않는 $4 \times 4$ 크기의 이미지를 한 patch로 나누고 각 patch를 flatten 시켜서 붙이면 아래와 같이 $\frac{H}{4} \times \frac{W}{4}$인 행렬로 변환이 된다.
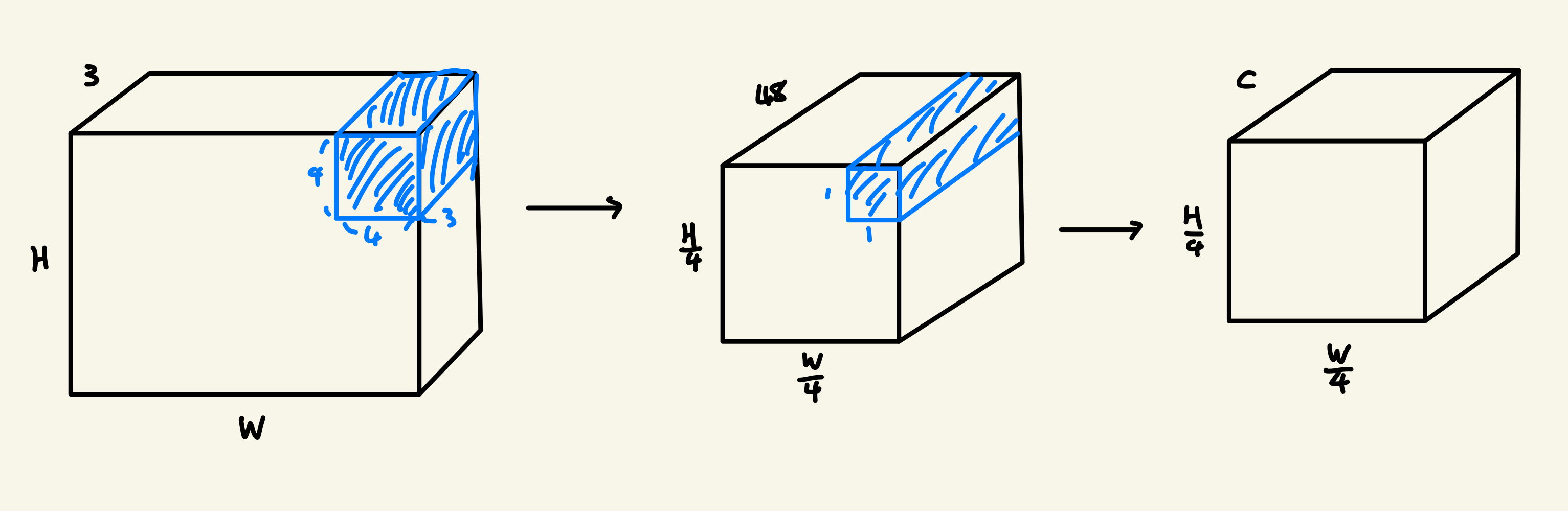
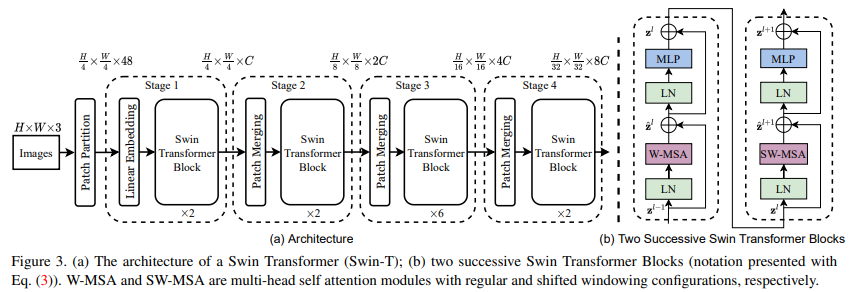
Figure 3(a)에서 stage 1을 보면 linear embedding이 있는데, 이 과정을 통해 channel이 48인 input을 정해진 상수 $C$로 channel 수를 바꿔준다. 그렇게 생성된 결과를 Swin Transformer Block에 넣는다. Swin Transformer Block은 위 Fig.3(b)에 나와있다. 전체 아키텍쳐 이미지를 보면 Swin Transformer Block 밑에 $\times 2$라고 써져 있는데, 이는 Swin Transformer Block이 두 개의 Block으로 구성되어 있기 때문이다. Swin Transformer Block에 대한 자세한 설명은 뒤에서 자세히 하겠다.
이렇게 Stage 1을 지나 나온 결과는 Stage 2에서 Patch Merging 과정을 거치게 된다. Patch Merging은 아래의 그림과 같은 방식으로 진행된다. (아래의 그림은 DSBA 유튜브 영상에서 캡쳐 했습니다.)
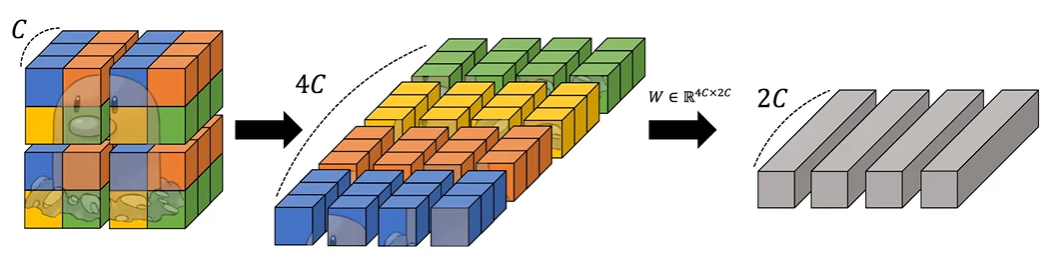
위 이미지에서 하나의 칸이 하나의 patch라고 하면 $2 \times 2$로 인접한 패치들을 연결하고 linear layer를 통해 $4C$를 $2C$로 축소시킨다. (논문에서는 축소시키는 이유는 나와있지 않다.) 그렇게 축소되서 나온 결과($\frac{H}{8} \times \frac{W}{8} \times 2C$)를 Swin Transformer에 넣는다.
이러한 과정을 Stage 3과 Stage 4에서도 반복한다. 논문에서는 이러한 단계는 공동으로 hierarchical representation을 생성하며, 일반적인 컨볼루션 네트워크와 동일한 feature map 해상도를 갖는다고 설명한다. 따라서 제안한 아키텍처는 다양한 비전 작업에서 기존 방법의 백본 네트워크를 편리하게 대체할 수 있다고 한다.
Swin Transformer Block

Swin Tranformer Block 하나는 위 이미지와 같이 구성되어 있고 위에서 MLP는 GELU activation을 사용하고 2-layer로 구성되어있다.
2.2 Shifted Window based Self-attention
기존의 Transformer는 토큰과 다른 모든 토큰 간의 관계를 계산하는 global self-attention를 수행한다. 이럴 경우 이미지의 해상도에 따라 quadratic하게 계산량이 증가한다. 이 때문에 고해상도의 고밀도 비전 작업을 하기에는 부적합하다.
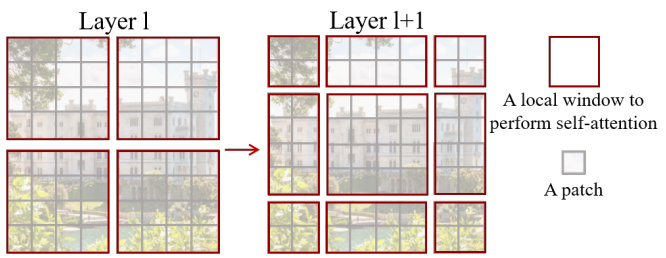
Self-attention in non-overlapped windows
효율적인 모델링을 위해 이미지 전체에 대한 self-attention을 계산하는 것이 아닌, $h \times w$ 이미지를 $M \times M$크기의 window로 나누어서 window내에서 self-attention을 계산하도록 하는 방식을 제안한다. 기존의 self-attention방식과 window방식을 도입한 self-attention방식의 계산 복잡도의 차이를 아래의 수식으로 논문에서 표현했다.
$$Ω(MSA) = 4hwC^2 + 2(hw)^ 2C,\quad (1)$$
$$Ω({\rm W-MSA}) = 4hwC^2 + 2M^2hwC,\quad (2)$$
두 수식을 보면 MSA는 $hw$에 quadratic하지만, window방식을 도입한 W-MSA는 $hw$에 선형적이다.
위 이미지에서 왼쪽이 window based self-attention을 나타낸 이미지이다.
Shifted window partitioning in successive blocks
위에서 설명한 방식인 window based self-attention을 하게되면 윈도우를 통해 잘린 부분끼리의 attention을 계산하지 않게 된다. 이렇게 되면 모델의 성능에 제한이 되는데 이를 해소하기 위한 윈도우 간의 연결을 도입하기 위해 shifted window partitioning 방식을 도입한다.
위 그림 layer l+1에서와 같이 규칙적으로 분할된 window에서 ($\lfloor \frac{M}{2} \rfloor ,\lfloor\frac{M}{2} \rfloor$) 픽셀만큼 window을 이동하여 이전 레이어의 window 구성에서 시프트된 window 구성을 채택한다. 그렇게 함으로써 window에 의해 잘려서 서로 self-attention 계산이 안된 부분을 서로 묶이게 하여 self-attention계산이 되도록 한다.
Efficient batch computation for shifted configuration
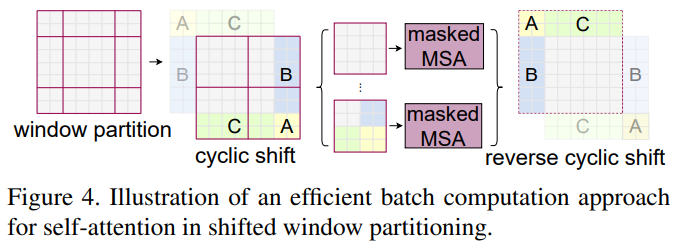

앞서 설명한 Shifted window를 수행하고 나면 Fig 4.에서 왼쪽 이미지가 된다. 이 window들의 크기는 제각각으로 $M \times M$ 보다 작아지는 것들이 생긴다. 이를 보완하기 위해 Fig 4.에서의 두 번째 이미지 처럼 cyclic shift를 수행하고 각 window를 masked MSA에 넣는다. 이 masked MSA를 통해 같은 window 내의 patch끼리는 self-attention을 계산하고 아닌 것들은 masking하면서 self-attention이 계산되지 않도록 한다. Fig 4. 밑에 있는 그림은 위 과정을 손으로 그려본 그림이다.
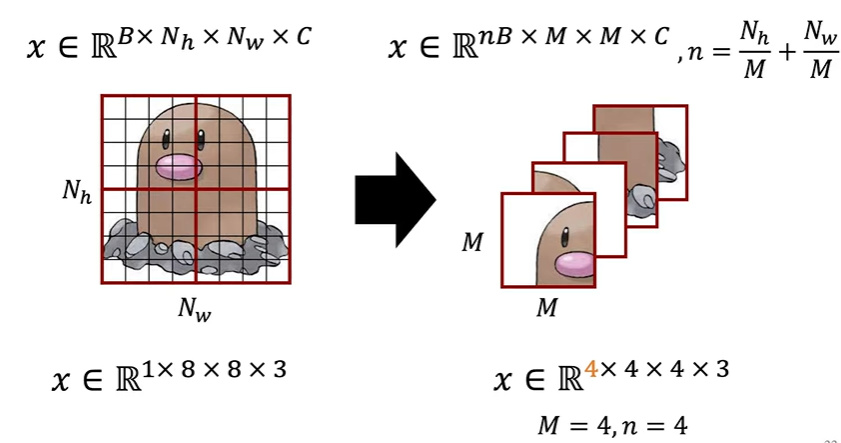
DSBA 논문 리뷰 영상에서는 window하나를 하나의 배치로 생각해 이미지 전체를 오른쪽과 같은 차원으로 변환해서 병렬적으로 계산해 더 효율적이라고 설명한다.
Relative position bias - > 이 부분은 제대로 이해하지 못했다...
이 부분은 논문 내용만으로는 이해가 되지 않아서 DSBA 논문 리뷰 영상을 토대로 이해를 했다. (논문만으론 이해하기 어려워서 영상을 보는 것을 추천한다!)

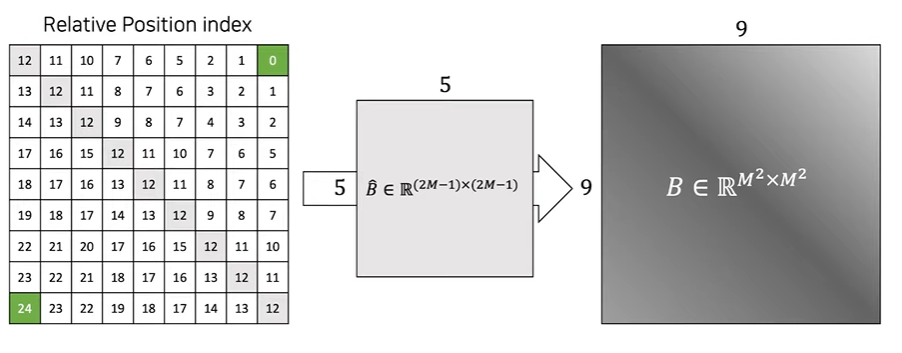
Relative Position Index는 window size(M)가 3이라 했을 때, 왼쪽 이미지에서 각 축(x축, y축)을 기준으로 각 원소마다의 거리를 나타내고 그 두 매트릭스에 모든 원소에 window size - 1을 더한다. 그리고 나서 x축 매트릭스의 각 원소에 2 * window size - 1를 곱해주고 x축 매트릭스와 y축 매트릭스를 더한다. 그렇게 되면 오른쪽 이미지의 0부터 24까지가 있는 매트릭스가 나오게 된다. 이렇게 되면 $\hat{B} \in \mathbb{R}^{(2m-1)\times(2M-1)}$ 매트릭스의 모든 인덱스를 나태낼 수 있고 $\hat{B}$에서 $B \in \mathbb{R}^{M^2 \times M^2}$를 뽑아 아래의 수식처럼 self-attention 계산에서 bias항을 추가해 상대적인 위치를 나타낼 수 있다. 이러한 방식으로 기존의 positional encoding을 대체하게 된다.
$${\rm Attention}(Q, K, V ) = {\rm SoftMax}(QK^T / \sqrt{ d} + B)V,\quad (4)$$
지금까지 Swin Transformer의 구조에 대해 알아봤다. 지금부터는 Swin Tranformer를 가지고 한 여러가지 실험에 대해 소개하겠다.
3. Experiments
논문에서 image classification, semantic segmentation, object detection에서의 각 sota 모델들과 비교한 실험을 진행했고 그 결과가 나와있다. Swin transformer가 여러 비전 task에서 좋은 성능을 냈다는 것이 매우 고무적이였다. 실험 셋팅과 그 결과는 이번 포스팅에서 다루지 않겠다.
3.1 Ablation Study
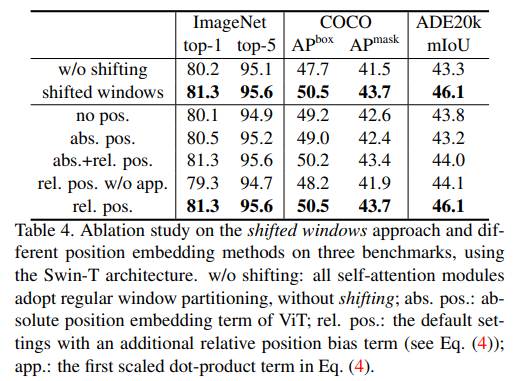
위 실험의 결과를 통해 shifted windows와 relative position bias가 모델 성능에 영향을 주는 것을 확인 할 수 있다.
4. Conclusion
Swin Transformer의 핵심 요소인 shifted window based self attention은 vision task에 효과적이고 효율적인 것으로 나타났으며, 자연어 처리 분야에서도 활용될 수 있기를 기대한다고 결론에 써놓고 논문을 마무리 했다.
이번 논문은 정리하는데 생각보다 많은 시간이 걸렸다. 중간중간에 이해하지 못하는 부분들이 많았고 논문만 보면 알 수 없는 부분들이 많았던 것 같다. 그래서 그런지 이번 논문 리뷰는 특히 더 어수선하게 쓴 것 같다ㅜㅜ
정말 많이 부족한 논문 리뷰였지만 읽어주셔서 감사합니다. 피드백은 언제나 환영입니다!!





