| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- flow matching
- 3d generation
- flipd
- diffusion model
- Python
- diffusion models
- rectified flow
- VirtualTryON
- Programmers
- transformer
- video generation
- 3d editing
- image editing
- inversion
- video editing
- BOJ
- 코딩테스트
- 논문리뷰
- DP
- 코테
- segmenation map generation
- Vit
- memorization
- noise optimization
- segmentation map
- diffusion
- 네이버 부스트캠프 ai tech 6기
- masactrl
- 프로그래머스
- visiontransformer
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] NeRF : Representing Scenes as Neural Radiance Fields for View Synthesis (ECCV 2020 oral) 본문
[평범한 학부생이 하는 논문 리뷰] NeRF : Representing Scenes as Neural Radiance Fields for View Synthesis (ECCV 2020 oral)
junseok-rh 2024. 6. 5. 16:15https://arxiv.org/abs/2003.08934
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
We present a method that achieves state-of-the-art results for synthesizing novel views of complex scenes by optimizing an underlying continuous volumetric scene function using a sparse set of input views. Our algorithm represents a scene using a fully-con
arxiv.org
랩실 인턴을 시작하기 전에 연구 주제에 대한 레퍼런스 논문들을 박사 멘토님들이 주셨고 그 중 하나가 바로 이번에 리뷰할 NeRF라는 논문이다. 3D관련 논문이 처음이다 보니 생소한 용어가 엄청 많았다ㅠㅠ. 그래도 연구 주제가 3D를 이용했기에 친해져야한다!! 이번에 논문을 읽기 전에 AMI LAB 발표 영상을 많이 참고했다. 설명을 너무 잘해주셔서 처음 접하는 분야지만 이해하기 쉬웠다.
이 NeRF라는 논문은 novel view synthesis를 다루는 논문이다. 간략히 설명하자면 여러 각도에서 본 이미지를 통해 아직 안본 각도에서의 이미지를 합성?하는 느낌으로 이해하면 될 것 같다. 부스트캠프를 하면서 이를 이용한 프로젝트를 한 팀의 NeRF 발표와 프로젝트 관련 얘기를 들은 적이 있는데 시간이 엄청 걸린다고 해서 서비스에 이용하기엔 힘들다고 들었던 것 같은데, 최신 기술 중에 보완이 많이 된 것들이 있을게 분명하다.
1. Neural Radiance Field Scene Representation
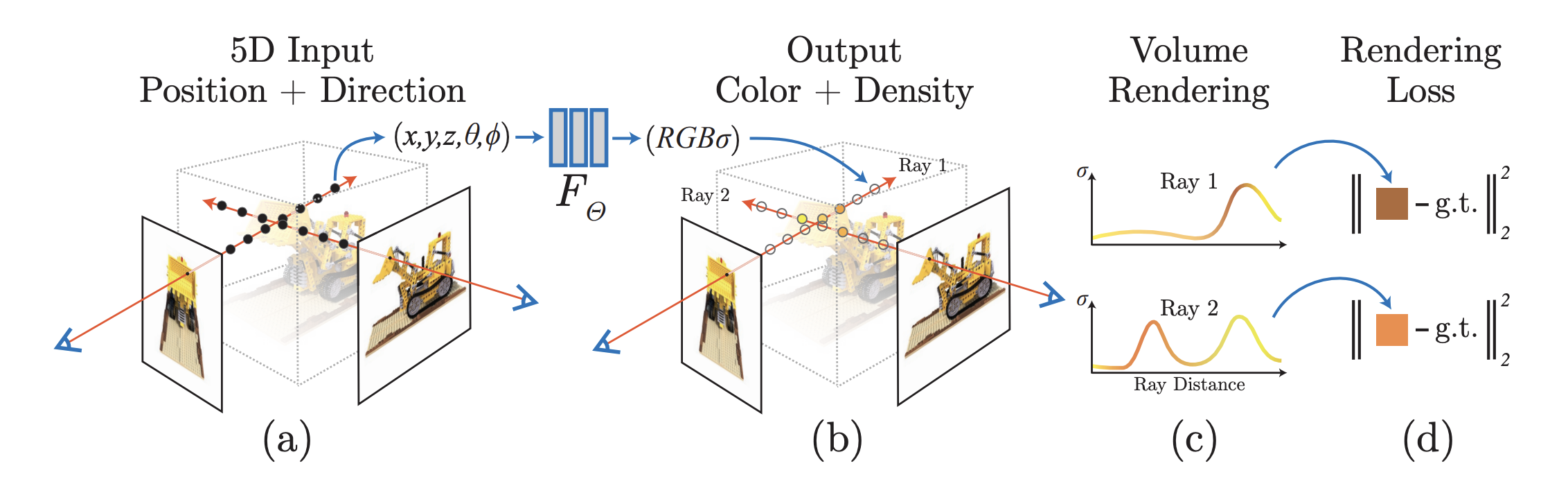
본 논문에서 continuous scene을 input이 3D location $\mathbb{x} = (x,y,z)$와 2D viewing direction $(\theta, \phi)$이고 output이 emitted color $\mathbb{c} = (r,g,b)$와 volum density $\sigma$인 5D vector-valued 함수로 표현한다. 실제로는 방향$\mathbb{d}$를 $(\theta, \phi)$로 표현하기 보다는 3D Cartesian unit vector로 표현한다고 한다. (3D Cartesian은 공간좌표로 발표영상에서 발표하시는 분 생각으로는 $\phi, \theta$로 공간좌표를 표현할 수 있으니까 그렇게 쓴 것 같다는데, 논문 abstract나 introduction에서 5D로 표현한다고 강조 해놓고... 왜...) 암튼 이를 통해 본 논문은 MLP network $F_{\Theta} : (\mathbb{x},\mathbb{d}) \rightarrow (\mathbb{c},\sigma)$를 이용해 continous 5D scene representation을 근사하고 weight $\Theta$를 input 5D coordinate를 그에 대응하는 volume density와 directional emitted color를 매핑함으로써 optimize한다.
본 논문에서는 multiview consistent를 위해 volume density $\sigma$는 location $\mathbb{x}$에 대한 함수로만, RGB color $\mathbb{c}$는 location과 viewing direction 둘 다에 대한 함수로 예측하도록 제한한다. 이를 성취하기 위해, MLP $F_{\Theta}$를 다음과 같은 구조로 만들었다.
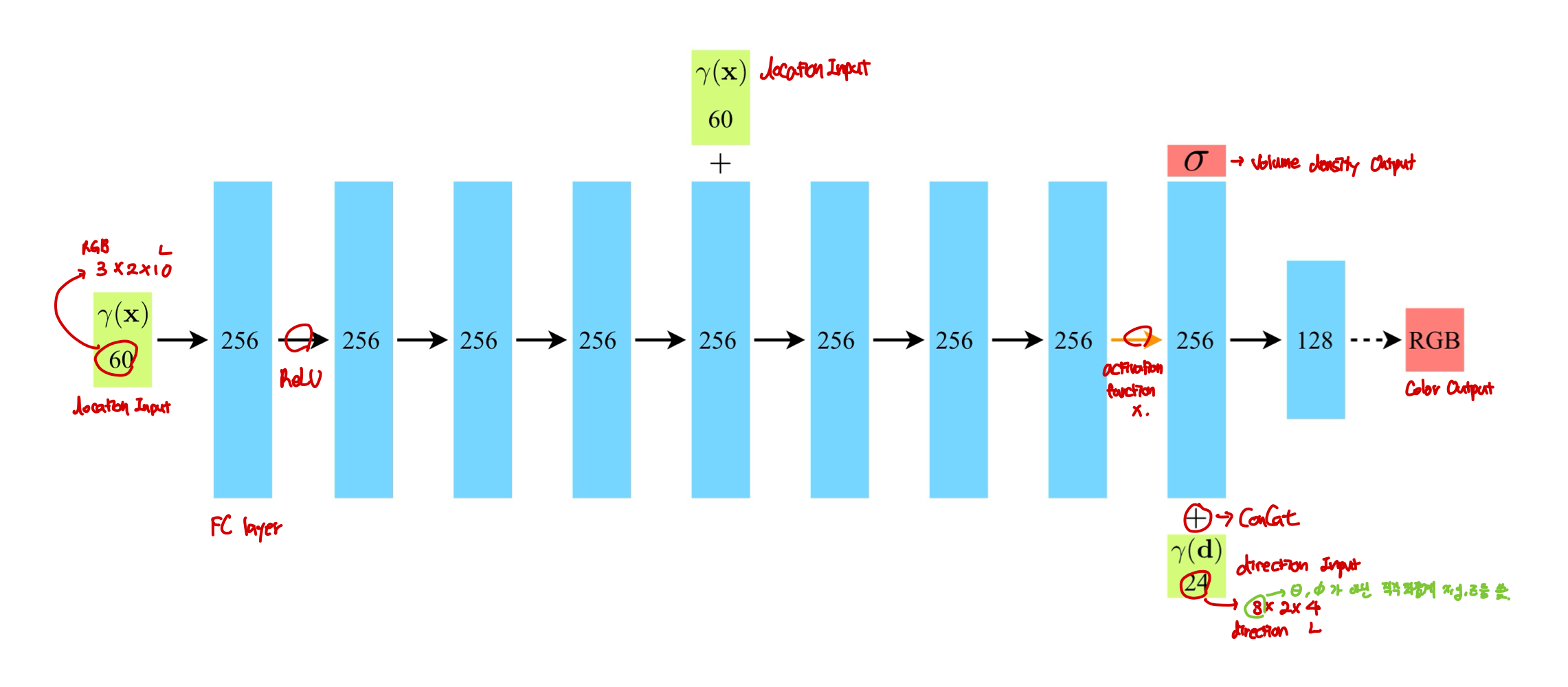
2. Volume Rendering with Radiance Fields
5D neural radiance field는 공간에서 어떤 지점의 volume density와 directional emitted radiance로 장면을 표현한다. 이 때, color를 classical volume rendering을 이용한다. 기대되는 color $C(\mathbb{r})$는 다음과 같은 수식으로 나타낸다.
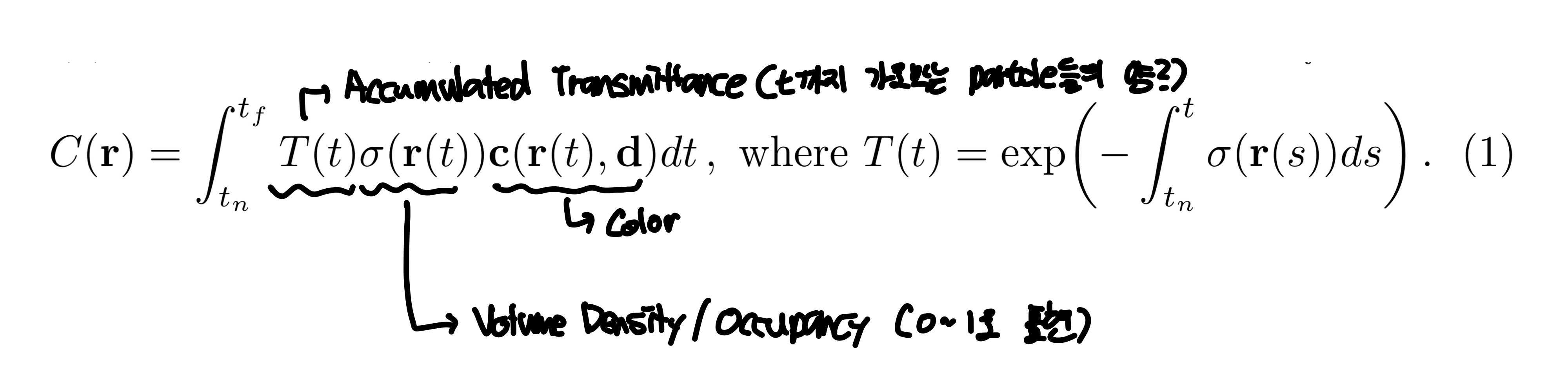
이 수식이 나타내는 것을 이미지로 나타내면 다음과 같다.
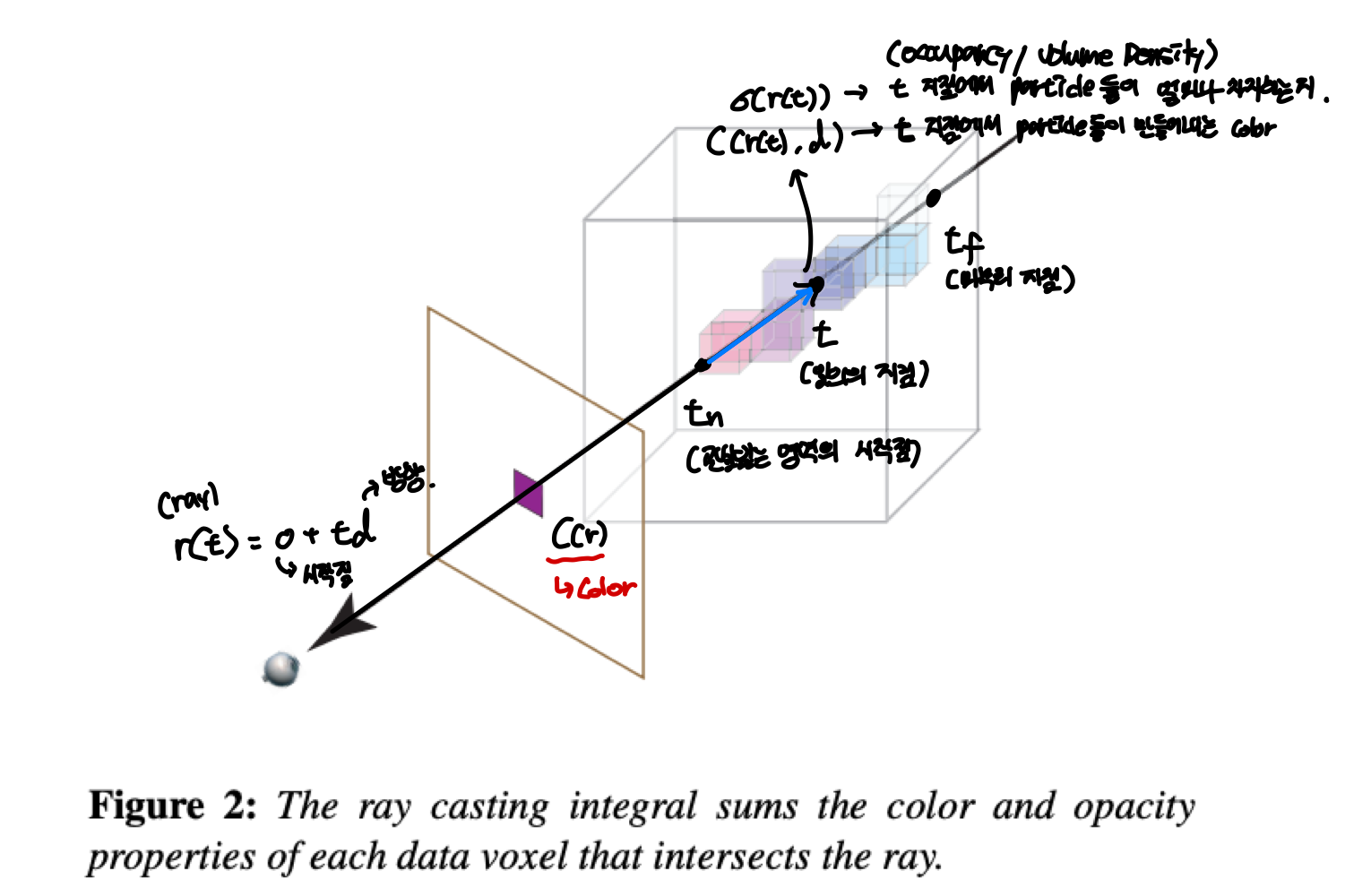
한 지점에서 3D 물체를 볼 때, 시작점 $o$에서 $\mathbb{d}$의 방향으로 보는 것으로 나타낼 수 있고 이 직선을 ray $r(t) = o + t\mathbb{d}$로 나타낼 수 있다. 이 직선을 따라 물체에 맞닿는 시작 부분 $t_n$과 끝 부분 $t_f$가 있을 것이고, 그 사이에 임의의 지점 $t$가 있을 것이다. 그렇다면 $t$에서의 $\sigma(r(t))$는 $t$ 지점에서 particle들이 얼마나 차지하는가(occupancy / volume density)를 나타내고 0~1사이의 값을 가진다. $\mathbb{c}(r(t), \mathbb{d})$는 $t$지점에서 particle들이 만들어내는 color를 나타낸다. 수식 1을 보면 적분하는 식의 맨 앞에 $T(t)$가 있는데 이는 accumulated trasmittance라고 한다. 이를 나타내는 식을 보면 $\sigma(\cdot)$을 $t$지점까지 적분하는 꼴인데 이는 처음 지점부터 $t$까지 누적한 volume density값을 이용한다. 그래서 $t$지점까지 얼마나 투명하냐를 나타내는 값을 $t$지점의 color와 volume density에 곱해서 처음 지점부터 끝 지점까지 적분해 rendering한 색 $C(r)$를 구한다.
여기서 모든 $t$에 대한 값을 구할 수 없기 때문에 2번 수식과 같이 샘플링을 하고,
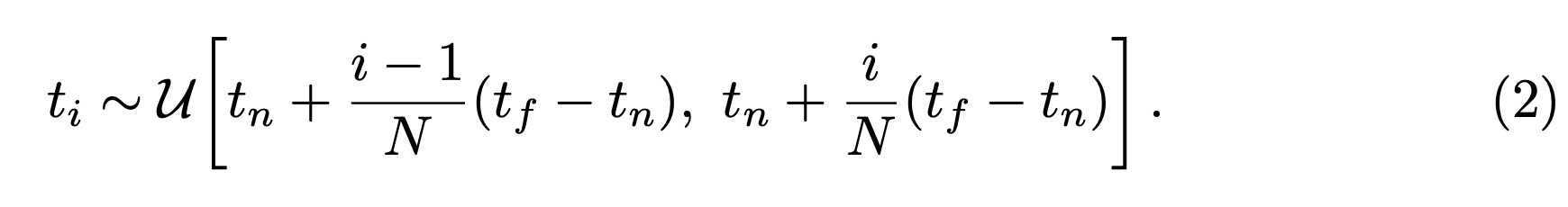
3번 수식으로 $C(r)$을 근사한다.
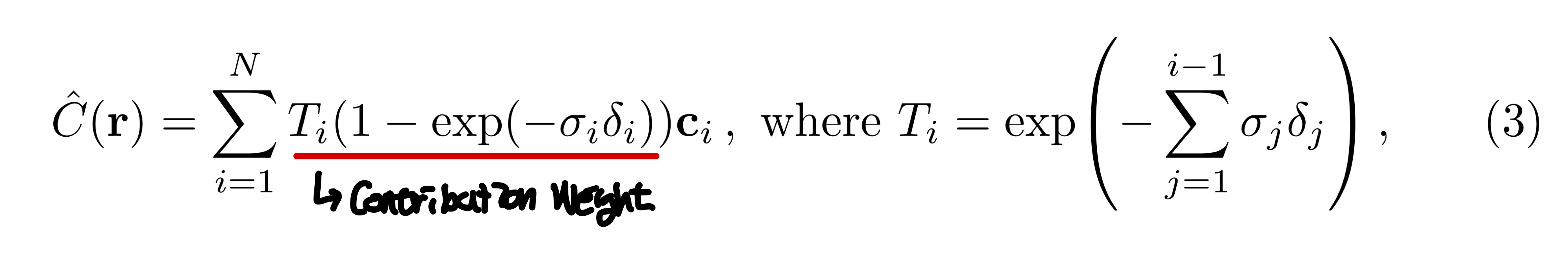
아래의 이미지는 위에서 바라본 경우를 나타낸 이미지이다.
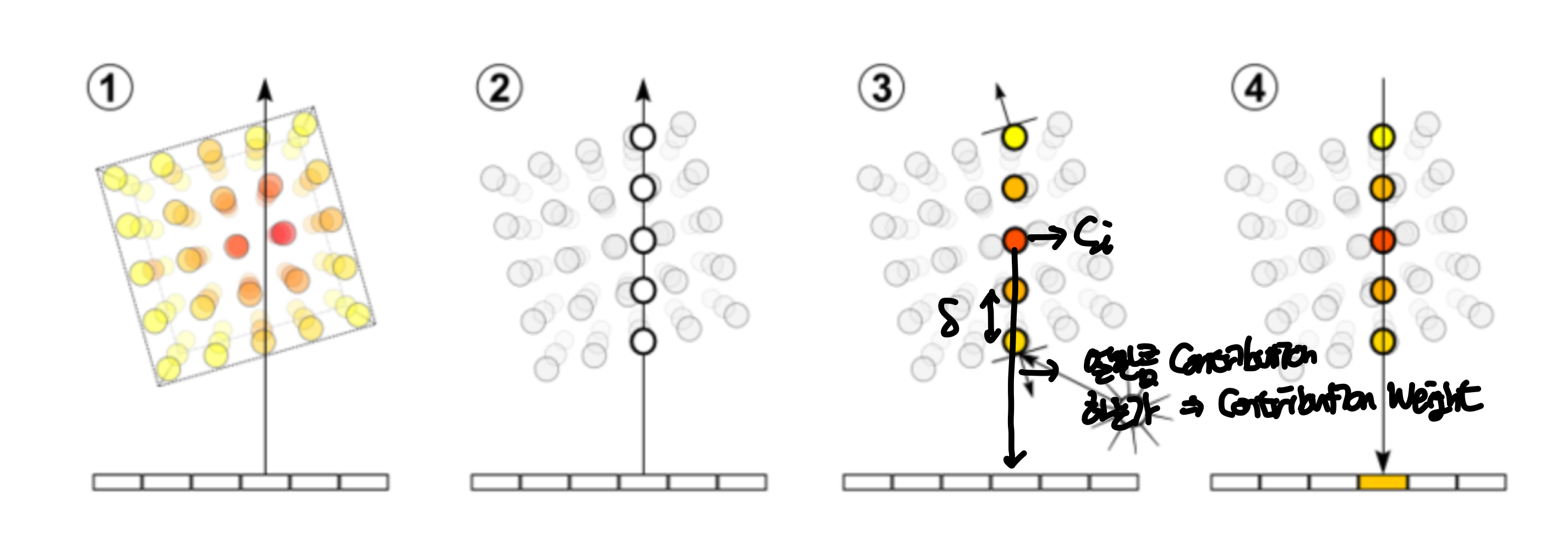
3번 수식을 보면 $C(r)$을 나타내는 수식 1과 다른 점은 $1-exp(\cdot)$으로 나타낸 것을 볼 수 있는데, 논문에서 알파값$\alpha_i = 1-exp(-\sigma_i \delta_i)$로 traditional alpha compositing으로 축소한다고 설명하는데 이건 질문을 해야할 듯 싶다...
아무튼 수식 3을 이용해서 근사화한 값을 통해 렌더링을 한다!
3. Optimizing a Neural Radiance Field
앞서 소개한 방식으로 novel view synthesis를 할 수 있지만 퀄리티가 그리 좋지 않다고 한다. 그래서 positional encoding과 hierarchical sampling을 제안한다.
3.1 Positional Encoding

MLP network $F_\Theta$에 $xyz\theta\phi$를 바로 넣어서 계산을 하게 되면 hign frequency를 잘 표현하지 못한다고 한다. 이는 이전 연구에서 deep network가 lower frequency function들을 학습하는데 편향된다는 연구와 일치하는 결과이다. 이 연구에서는 또한 network를 통과하기 전에 high frequency functions를 사용해 input을 더 높은 차원의 공간으로 맵핑하는 것이 high frequency variation을 포함한 데이터에 더 잘 맞는다는 것을 보였다. 이를 통해 본 논문에서는 $F_\Theta$를 $F_\Theta = F_{\Theta}^\prime \circ \gamma$로 reformulate한다.
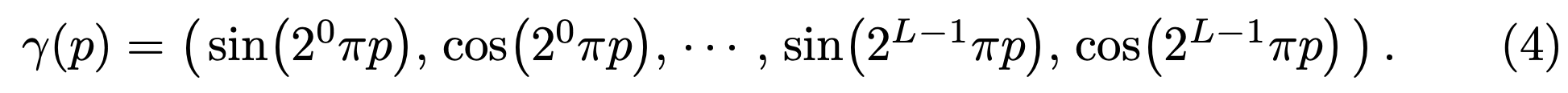
이는 $\mathbb{x}$와 $\mathbb{d}$에 각각 적용되는데, 실험에서는 $\mathbb{x}$에는 $L = 10$, $\mathbb{d}$에는 $L = 4$가 적용된다.
Positional encoding은 Transformer에서도 사용되지만 본 논문에서와 의미는 다르다. 본 논문에서는 MLP가 higher frequency function을 더 쉽게 근사하기 위해 continuous input coordinates를 더 고차원의 공간으로 맵핑하기 위해 사용한다.
3.2 Hierarchical Volume Sampling
렌더링된 이미지에 기여하지 않는 여유 공간과 가려지는 영역에서 샘플을 줄이고 기여를 많이 하는 부분에서 샘플링을 주로 하기 위해 hierarchical volume sampling을 도입한다.
Single Network를 사용하기 보다는, "coarse"와 "fine" network를 동시에 optimizing한다. 수식 2,3을 이용해 먼저 $N_c$개의 location을 샘플링해서 coarse network를 평가한다. 수식 3을 아래와 같이 다시 쓸 수 있다.
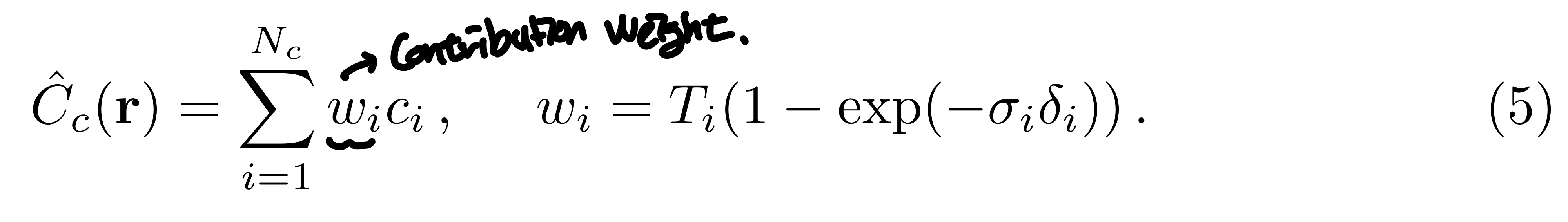
여기서 contribution weights를 $\hat{w}_i = \frac{w_i}{\Sigma^{N_c}_{j=1}w_j}$로 normalizing하면 이는 일종의 PDF와 같아진다. $\hat{w}$의 분포에서 Inverse transform sampling을 통해 $N_f$개의 locations를 샘플링한다. $N_c + N_f$개의 sample을 이용해 "fine" network를 평가한다.
Inverse Transform Sampling
어떤 분포의 CDF는 0~1 사이의 값을 가진다. 샘플링하기 어려운 분포에서 샘플링을 하고 싶을 때, uniform 분포에서 샘플링을 하고 그 값들을 어떤 분포의 CDF의 역함수에 넣어 나온 값들은 그 분포에서 샘플링한 것과 같다는 그런 샘플링 방식이다. 수리통계 시간 때 배운 내용을 대충 요약해보자면 이렇다.
3.3 Implementation Details
NeRF의 loss 함수는 다음과 같다.
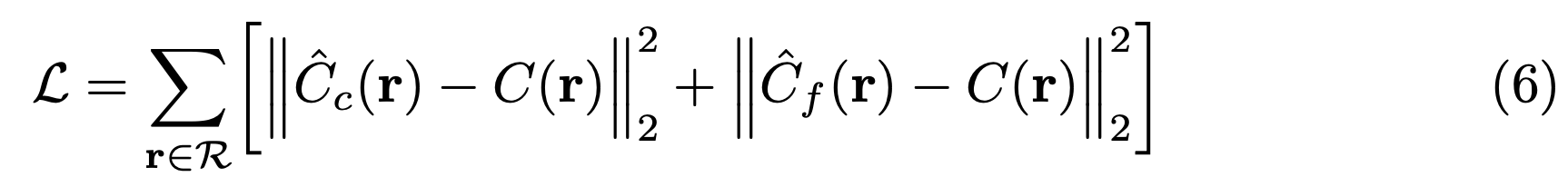
여기서 $C(\mathbb{r})$는 ground truth, $\hat{C}_c(\mathbb{r})$는 coarse volume, $\hat{C}_f(\mathbb{r})$는 fine volume을 나타낸다. 이 때, $\hat{C}_c(\mathbb{r})$의 loss도 최소화하는데 이 이유는 coarse network로부터의 wieght distribution이 fine network에서 샘플들을 할당하는데 사용되기 때문이라고 설명한다.

4. Results
4.1 정량적인 결과
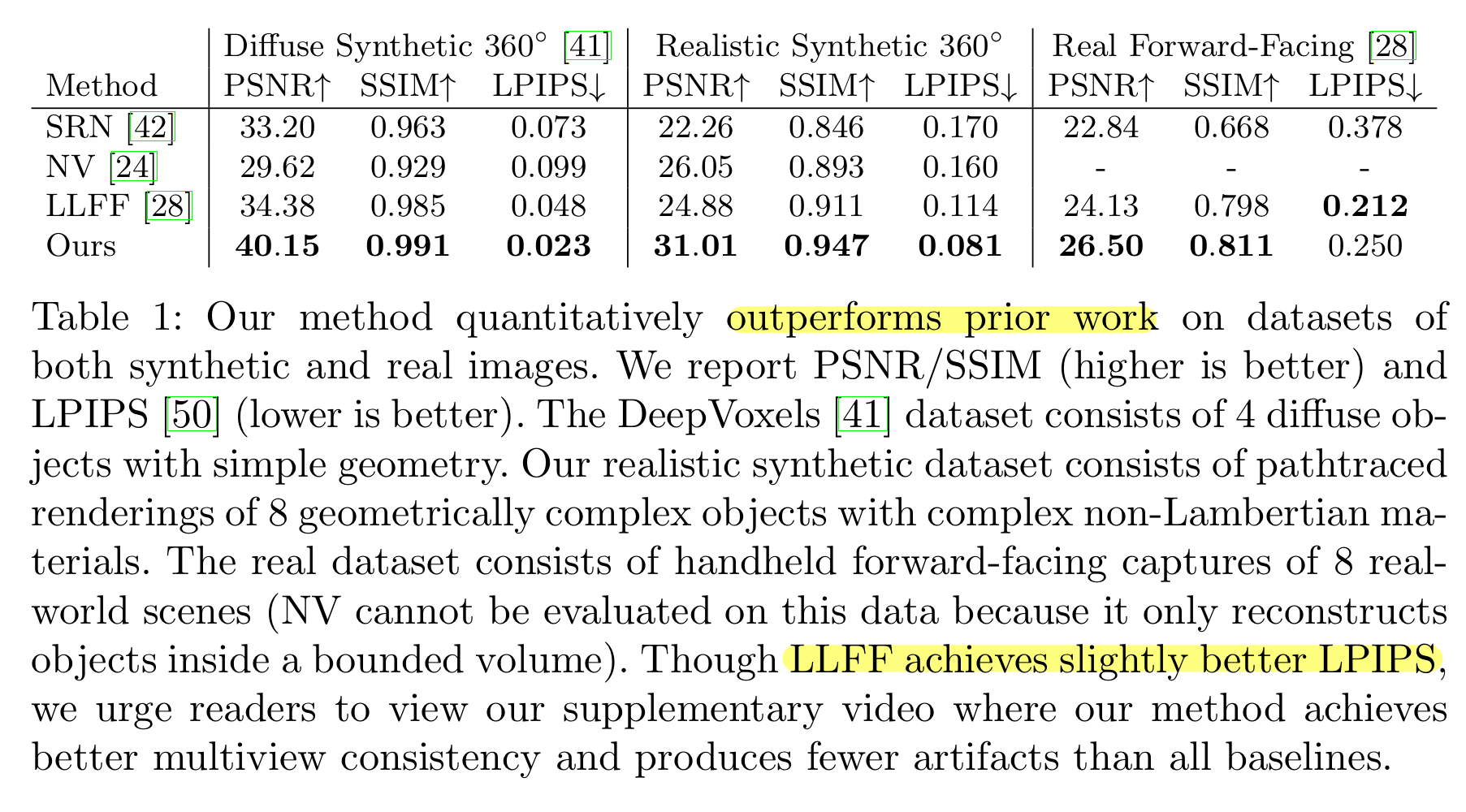
여기서 LLFF모델의 Real Forward-Facing데이터셋에 대한 결과를 보면 LPIPS가 더 좋은 것을 볼 수 있는데, 이는 LLFF가 forward-facing이라는 특수한 경우에 맞게 디자인된 모델이기에 좀더 좋은 결과를 보인 것으로 생각된다. 이 외에는 다 NeRF의 결과가 더 좋은 것을 볼 수 있다.
4.2 정성적인 결과


4.3 Ablations
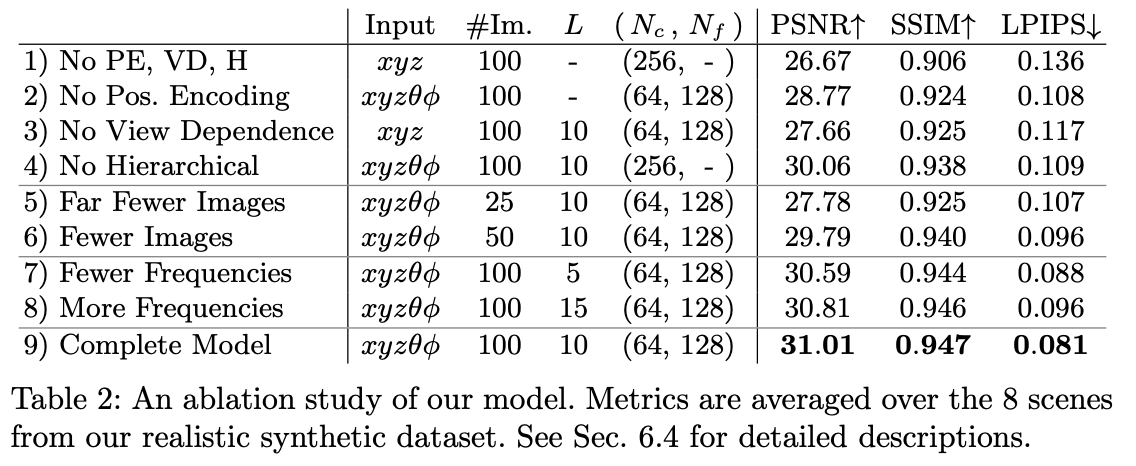
첫 3D관련 논문인데 생소하고 모르는 부분이 많았다. 랩 미팅을 진행하면서 질문도 많이 하고 공부를 열심히 해야할 듯 싶다....




