| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- masactrl
- 3d editing
- Programmers
- 3d generation
- Python
- BOJ
- segmenation map generation
- diffusion models
- Vit
- noise optimization
- transformer
- VirtualTryON
- diffusion model
- 코딩테스트
- rectified flow
- segmentation map
- video generation
- memorization
- 프로그래머스
- 코테
- visiontransformer
- flow matching
- diffusion
- image editing
- DP
- flipd
- 논문리뷰
- 네이버 부스트캠프 ai tech 6기
- video editing
- inversion
- Today
- Total
평범한 필기장
[평범한 학부생이 하는 논문 리뷰] 3D Gaussian Splatting for Real-Time Radiance Field Rendering (SIGGRAPH 2023) 본문
[평범한 학부생이 하는 논문 리뷰] 3D Gaussian Splatting for Real-Time Radiance Field Rendering (SIGGRAPH 2023)
junseok-rh 2024. 6. 10. 01:08https://arxiv.org/abs/2308.04079
3D Gaussian Splatting for Real-Time Radiance Field Rendering
Radiance Field methods have recently revolutionized novel-view synthesis of scenes captured with multiple photos or videos. However, achieving high visual quality still requires neural networks that are costly to train and render, while recent faster metho
arxiv.org
1. Introduction
NeRF 기반의 방식들은 high quality의 novel scene synthesis가 가능하지만 시간이 오래 걸리기에 real-time 렌더링에서 한계점을 드러낸다. 또한 다른 방식들은 quality-time trade-off를 지녀서 시간은 빠르지만 퀄리티가 NeRF와 같은 모델처럼 high quality가 아니다. 이러한 점을 해결하기 위해 본 논문은 3D Gaussian Splatting을 제안하면서 기존 SOTA인 Mip-NeRF360만큼의 성능이 나오면서 InstantNGP만큼의 학습 속도를 지닌다고 말한다.
3D Gaussian Splatting은 크게 3가지로 구성되어 있다고 한다.
- Structure-from-Motion(SfM)을 통해 얻은 sparse point cloud를 초기값으로 3D Gaussian들을 도입
- 3D position, opacity $\alpha$, anisotropic covariance, spherical harmonic(SH) coefficients의 최적화
- Tile-based rasterization에서 영향을 받은 빠른 GPU sorting 알고리즘으로 통한 real-time rendering
3D Gaussian Splatting은 이전의 implicit radiance field 접근법들과 동등하거나 더 좋은 퀄리티의 보여준다. 또한 이전의 가장 빠른 방식과 유사한 학습 속도와 퀄리티를 보여주며 고수준의 novel-view synthesis에 대한 real-time rendering을 처음으로 제공한다.
2. Overview


3. Differentiable 3D Gaussian Splatting
본 논문에서 normal(표면 법선)이 없는 (SfM) 포인트들의 sparse한 셋으로 부터 시작해서 고수준의 novel view synthesis를 가능하게 하는 scene representation을 최적화하는 것이 목표이다. 이를 위해 differentiable volumetric representation의 특징을 상속받는 동시에 빠른 렌더링을 위해 unstructured이고 explicit한 primitive를 필요로 한다. 본 논문에서는 미분가능하고 2D splats로 쉽게 project되는 3D Gaussian을 선택해 빠른 렌더링을 위한 빠른 $\alpha$-blending을 가능하게 했다.
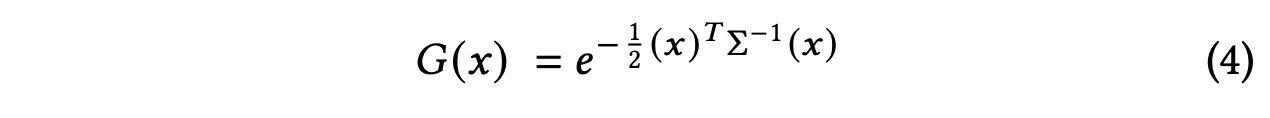
3D gaussian은 point(mean) $\mu$에 centered되고 full 3D convariance matrix $\Sigma$로 위와 같이 정의된다. 렌더링을 위해 3D gaussian을 2D로 project를 시켜야하기 때문에, viewing transformation $W$가 주어지면 카메라 coordinates에서 covariance matrix $\Sigma^\prime$은 다음과 같다.

여기서 $J$는 viewing transformation $W$의 affine approximation의 Jacobian이다.
Covariance matrix $\Sigma$는 positive semi-definite일 때만 최적화가 가능하므로 최적화가 어렵다고 한다. 그래서 본 논문에서는 더 직관적이고 최적화를 위해 동등하게 expressive한 representation을 선택한다. 3D Gaussian의 covariance matrix $\Sigma$는 타원체의 구성을 설명하는 것과 유사하다. Scaling matrix $S$와 rotation matrix $R$가 주어지면 대응되는 $\Sigma$를 다음과 같이 찾을 수 있다.

각 요소들을 독립적으로 최적화하기 위해, 스케일링을 위해 3D vector $s$와 rotation을 표현하기 위해 quaternion $q$로 각각 따로 저장한다. 이들은 각각의 행렬로 쉽게 변환될 수 있으며, 합쳐질 때는 $q$를 정규화하여 유효한 단위 쿼터니언을 얻는 것을 확실히 해야 한다.
학습 동안 자동 미분 때문의 overhead를 피하기 위해, 모든 파라미터에 대한 gradient들을 명시적으로 유도한다.
최적화에 적합한 anisotropic covariance의 representation은 capture된 장면의 다른 모양들의 geometry에 적응하도록 3D Gaussian들을 최적화하도록 한다.
4. Optimization with Adaptive Density Control of 3D Gaussians
본 논문의 접근법의 core는 free-view synthesis 를 위해 장면을 정확하게 표현하는 3D Gaussian의 dense set을 만드는 최적화 스텝이다. Position $p$, $\alpha$, convariance $\Sigma$ 뿐만 아니라, 장면의 view-dependent appearance를 정확하게 캡쳐하기 위해 각 Gaussian의 색 $c$를 표현하는 SH coefficients 또한 최적화한다. 최적화는 Gaussian density를 제어하는 스텝이 끼워져서 진행된다.
4.1 Optimization
Geometry는 3D를 2D로 투영하는 데에서의 모호함에 의한 잘못 위치될 수 있기 때문에, optimization은 geometry를 생성하고 잘못 위치되면 파괴하거나 이동시킬 수 있어야한다. 3D Gaussian의 covariance parameter의 퀄리티는 거대한 homogeneous area들은 적은 수의 큰 anisotropic Gaussian들로 캡쳐될 수 있기 때문에 representation의 compactness에 중요하다.
본 논문에서는 SGD를 사용하고 몇 operation들에 대해서는 CUDA kernel을 사용한다. 특히 빠른 rasterization은 optimization의 효율성에 중요하다. 이는 optimization의 main computational bottleneck이기 때문이다.
$\alpha$에 대해서는 sigmoid 함수를, covariance의 scale에 대해서는 exponential activation 함수를 활성화 함수로 사용한다.
초기 covariance matrix는 가장 가까운 세 점까지의 거리의 평균을 축으로하는 isotropic Gaussian으로 추정한다. Position에 대해서만 exponential decay 스케줄링을 사용한다. Loss 함수는 다음과 같다.
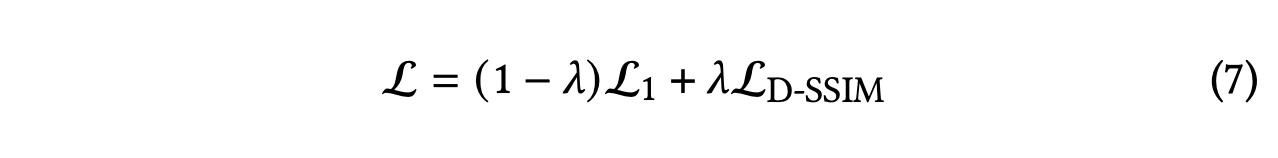
이 때 $\lambda = 1$을 사용한다.
D-SSIM이란?
D-SSIM은 이미지의 구조적 유사성을 측정하는 메트릭으로 SSIM에 디스톡션을 추가하여 이미지의 왜곡을 더 잘 반영한다고 한다. 미분이 가능해서 평가 메트릭뿐만 아니라 loss로도 사용 가능하다고 한다.

그렇다면 SSIM이란?

위 수식을 통해 이미지 $x$와 $y$를 비교하는 메트릭으로 이미지의 밝기, 대조, 구조 세 가지 측면을 고려하여 두 이미지 간의 유사성을 측정한다고 한다.
4.2 Adaptive Control of Gaussians
SfM으로부터의 초기의 sparse points의 셋으로 시작하고 그 후로 본 논문의 방식을 unit volume에 대해 Gaussian들의 수와 그들의 density를 adaptively하게 조정하도록 적용한다. 이를 통해 scene을 더 잘 표현하도록 점진적으로 최적화한다. 100 iter마다 densify하고 $\alpha$가 $\epsilon_\alpha$보다 작은 Gaussian을 제거한다.
Adaptive control of the Gaussians는 빈 공간을 채우는 것을 필요로 하는데, missing geometric feature를 가진 지역(under-reconsturction)과 Gaussian이 scene에서 너무 넓은 지역을 cover하는 지역(over-reconstruction)에 집중한다. 이 두가지 경우 모두 큰 view-space positional gradient를 가진다. 이러한 지역이 아직 잘 reconstruction이 되지 않았기에 optimization을 통해 이 지역의 Gaussian을 이동시킨다. 이 때의 threshold는 $\tau_{pos} = 0.0002$로 test를 진행했다.
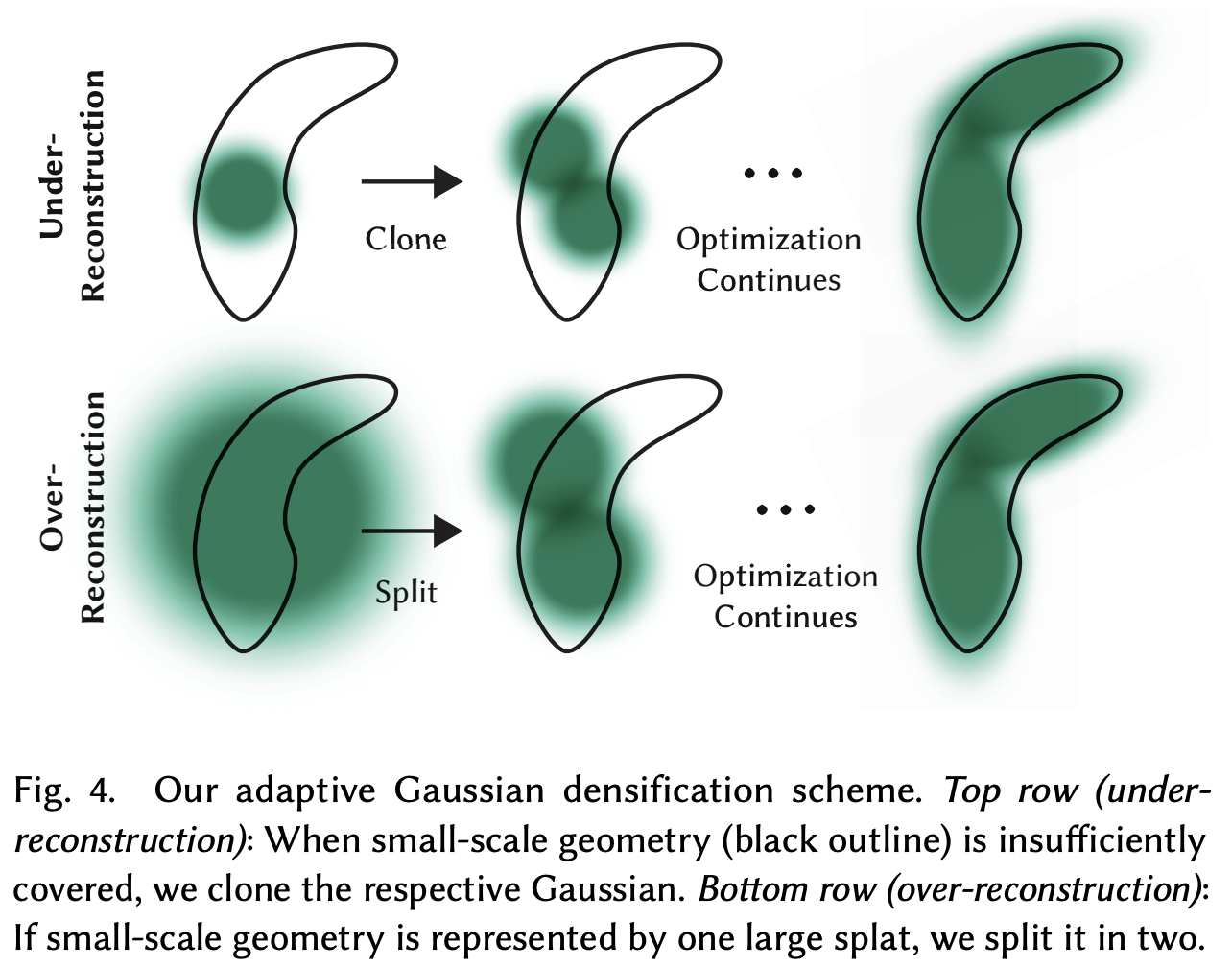
Under-reconstruction의 경우 동일한 크기의 gaussian을 복제하고 이를 positional gradient 방향으로 이동시킨다. Over-reconstruction의 경우 $\phi = 1.6$으로 scale을 나눈 두개의 Gaussian으로 대체한다. 그들의 위치는 기존의 3D gaussian을 PDF로 샘플링해서 초기화한다.
본 논문의 optimization은 input 카메라에 가까운 floater에 의해 Gaussian density에 대한 unjustified increase를 야기된다. 이 현상을 완화하기 위한 효과적인 방식은 3000 iter마다 $\alpha$값을 0에 가깝게 설정하는 것이다. 최적화는 필요한 곳에서 Gaussian들에 대해 $\alpha$를 증가시고 $\epsilon_\alpha$보다 작은 $\alpha$를 가진 Gaussian들을 제거하는 culling 접근법을 사용할 수 있다. Gaussian들은 줄어들거나 커질 것이고 서로 상당히 겹치게 된다. 본 논문은 주기적으로 world space에서 거대한 Gaussian들과 viewspace에서 큰 footprint를 가진 Gaussian들을 제거한다.
5. Fast Diffenrentiable Rasterization for Gaussians
본 논문의 목표는 대략적인 $\alpha$-blending을 가능하게 하고 이전 연구에 존재하던 gradient를 얻을 수 있는 splat들의 수에 대한 강한 제약을 피하는 빠른 전체적인 렌더링과 빠른 sorting을 가지는 것이다. 이러한 목표를 달성하기 위해 본 논문은 tile-based rasterization for Gaussian splats를 제안한다.
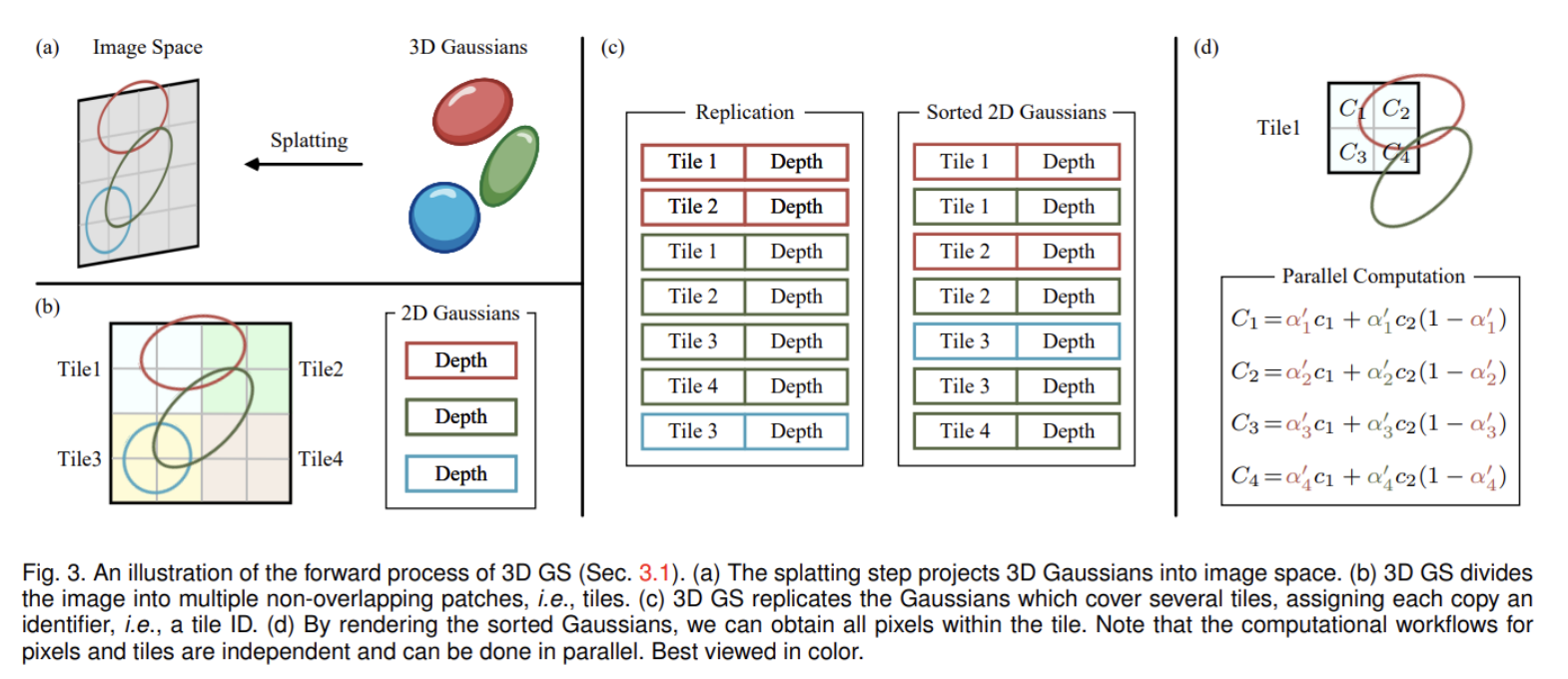
Screen을 16*16으로 나누고 view frustum과 각 타일에 대해 3D Gaussian들을 cull한다. 여기서 낯선 단어들이 있어서 간단히 정리하면 아래와 같다.
- view frustum : 시야각?으로 이해했다.
- cull : view frustum 밖에 있는 것들을 제거하는? 느낌으로 이해했다.
이를 바탕으로 위 문장을 다시 이해해보면 view frustum외에 있는 것들을 제거하는 절차 진행했다고 받아들였다. 여기서 16*16으로 나눈 이유는 각 타일마다 다른 GPU thread에서 계산해서 빠르게 계산하기 위함으로 이해했다. 또한 guard band를 이용해 극단적인 위치(너무 가깝거나 먼)에 있는 gaussian들 또한 제거했다고 한다.(이들의 projected 2D covariance를 계산하는 것은 불안정적) 그런 후에 위 그림에서 (c)와 같이 gaussian들 마다 속한 tile과 depth에 따라 key를 부여한다. 그러고 이를 GPU Radix sort를 이용해 정렬을 해준다. 그리고 각 타일마다 front-to-back으로 color와 $\alpha$값을 accumulate해서 픽셀 값을 구한다.

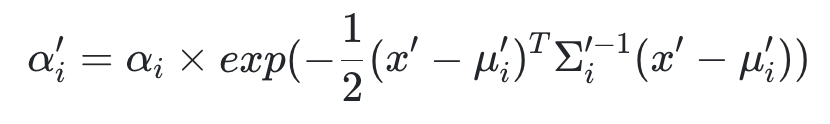
여기서 $c_i$는 학습된 color이고, $\alpha$는 학습된 opacity이다. $\alpha$값이 saturation되면 그 thread는 멈춘다.
전체적인 rasterization 알고리즘은 아래와 같다.

6. Results and Evaluation
6.1 Results and Evaluation

데이터셋에 따라 결과는 다르지만 SOTA이상의 퀄리티를 내면서 좋은 Training time과 FPS를 보인다.
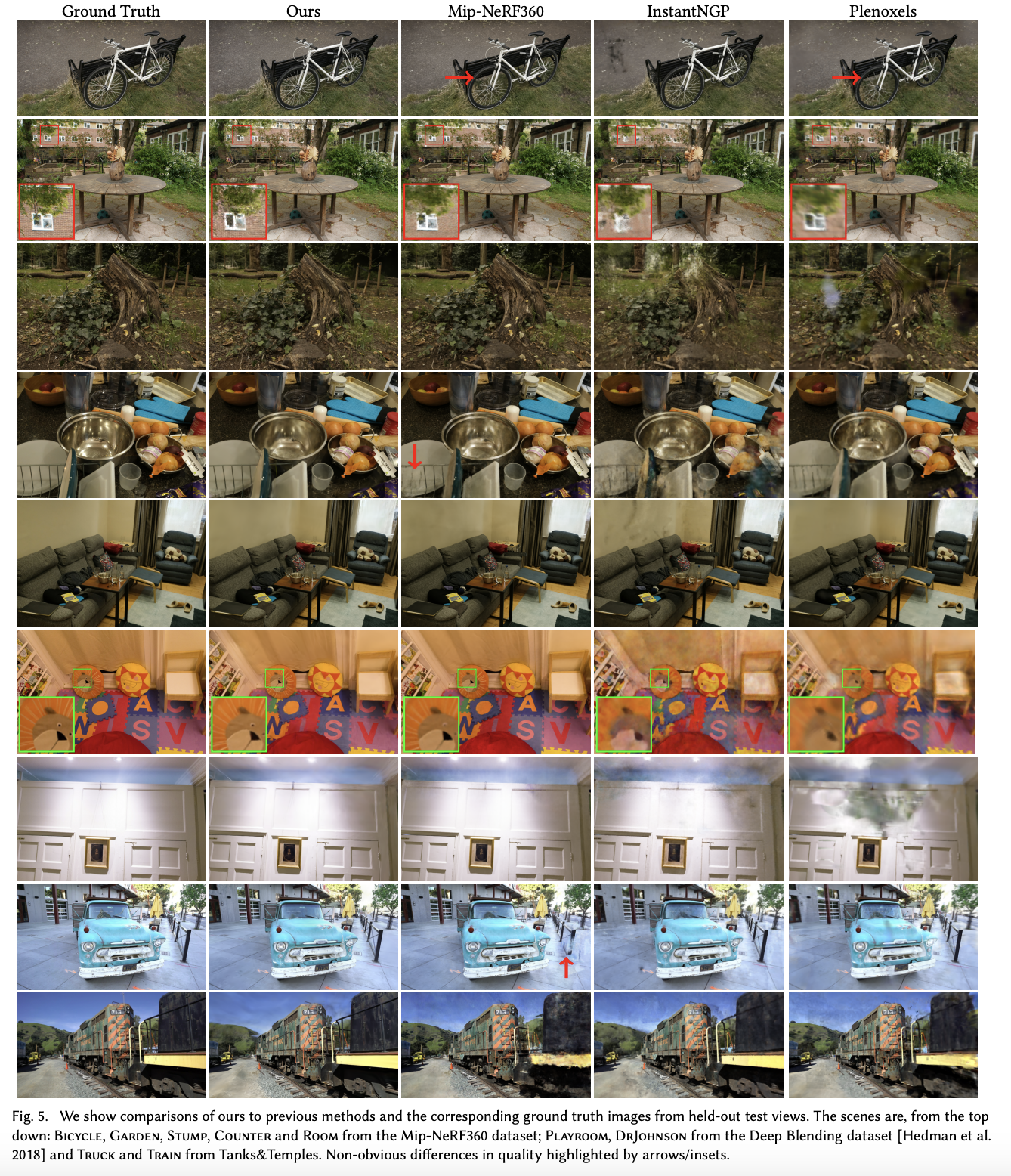
위 결과를 보면 Mip-NeRF360에서 보이는 artifact들이 본 논문의 결과에서는 보이지 않는 것을 볼 수 있다.
6.2 Ablations
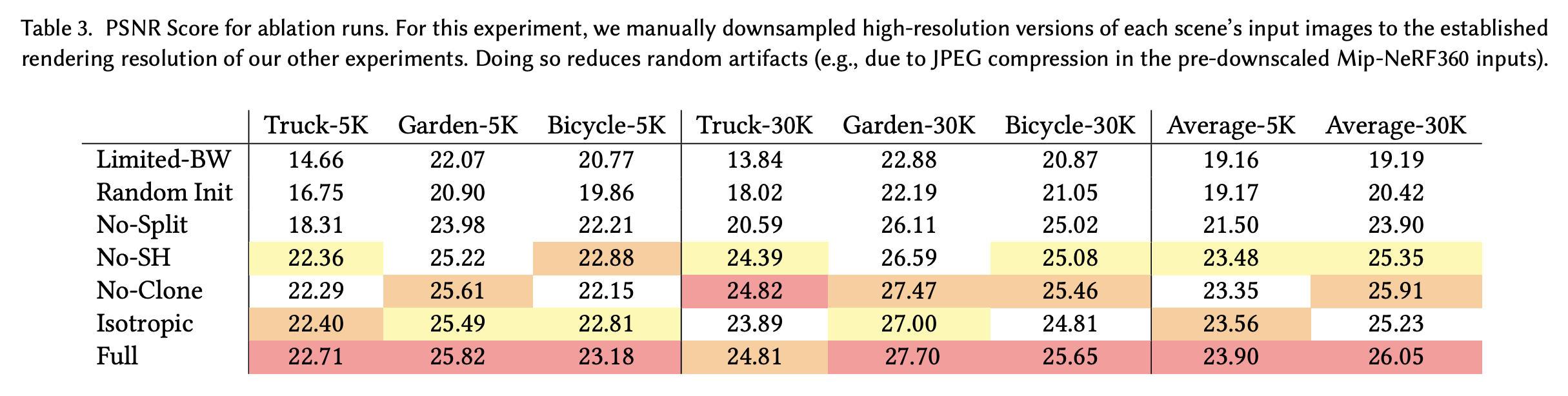
Initialization from SfM

Random point cloud로 초기화를 한 경우 배경에서 결과가 안좋았고, 학습 시에 잘 다루지 않은 공간에서 더 많은 floater들을 보이는 것을 보였다.
Densification

큰 가우시안을 split하는 것은 배경의 좋은 reconstruction에 중요하고, 작은 가우시안을 cloning하는 것은 특히 얇은 구조가 있는 장면에서 수렴이 빠르고 잘되는게 한다.
Unlimited depth complexity of splats with gradients

$N$개의 가장 앞에 있는 점들에 대해서만 gradient를 계산하고 나머지는 건너뛰는 방식이 속도는 빠르게하고 퀄리티는 보존하는지에 대해 실험했지만 결과는 위와 같이 원래와 차이가 많이 난다.
Anisotropic Convariance

3D Gaussian의 모든 축을 하나의 값으로 control하는 것과 비교해 실험을 진행했고 결과는 위와 같다. 퀄리티 차이가 심한 것을 볼 수 있다.
Spherical Harmonics
View-dependent 효과에 대해 보상하기 때문에 위 표와 같은 PSNR 결과를 보여준다.
6.3 Limitations
- 이전의 방식들과 유사하게 잘 관측되지 않은 장면은 artifact들이 존재
- 이전의 방식들과 유사하게 늘어지고 얼룩진 artifact를 생성할 수 있음
- 최적화에서 거대한 Gaussian이 만들어지면 popping artifacts 가끔 발생
- 최적화에서 regularization을 적용하지 않음
- NeRF-based 기법들보다 memory consumption이 상당히 높음.
이번 논문은 부스트캠프를 진행하면서 멘토님이 관심 있으면 읽어보라고 하신 논문이지만 이제야 읽게 됐다. 이 분야에 대한 사전지식이 많이 부족하다 보니 논문을 읽으면서 이해 못한 부분이 엄청 많았다... 이대로 랩실 인턴 진짜 시작하면 아무 것도 못할 것 같아서 너무 걱정이다...




